练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点I为△ABC的内心，AB=4，AC=3，BC=2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为（　　）

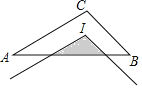
    A. 4.5 B. 4 C. 3 D. 2

    【答案】B

    【解析】连接AI、BI，因为三角形的内心是角平分线的交点，所以AI是∠CAB的平分线，由平行的性质和等角对等边可得：AD=DI，同理BE=EI，所以图中阴影部分的周长就是边AB的长．

    连接AI、BI，

    ∵点I为△ABC的内心，

    ∴AI平分∠CAB，

    ∴∠CAI=∠BAI，

    由平移得：AC∥DI，

    ∴∠CAI=∠AID，

    ∴∠BAI=∠AID，

    ∴AD=DI，

    同理可得：BE=EI，

    ∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=4，

    即图中阴影部分的周长为4，

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】综合与实践：折纸中的数学

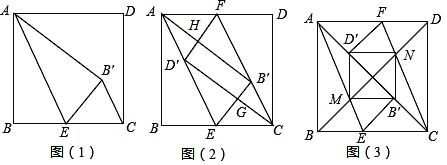
    问题情境：数学活动课上，老师让同学们折叠正方形纸片ABCD进行探究活动，兴趣小组的同学经过动手操作探究，提出了如下两个问题：

    问题1：如图（1），若点E为BC的中点，设AE将正方形纸片ABCD折叠，点B的对应点为B′，连接B′C，求证：B′C∥AE．

    问题2：如图（2），若点E，点F分别为边BC，边AD的中点，沿AE、CF将正方形纸片ABCD折叠，点B的对应点为B′，点D的对应点D′，D′F与AB′交于点H，B′E与CD′交于点G，求证：四边形D′GB′H为矩形．

    （1）解决问题：请你对兴趣小组提出的两个问题进行证明．

    （2）拓展探究：解决完兴趣小组提出的两个问题后，实践小组的同学们进行如下实践操作：如图（3），点E，点F分别为BC、AD上的点，将正方形纸片沿AE、CF折叠，使得点B落在对角线上的点B′处，点D落在对角线AC上的点D′处，AE与对角线BD的交点为M，CF与对角线BD的交点为N，分别连接MB′，B′N，D′N，D′M．他们认为四边形MB′ND′为正方形．

    实践小组的同学们发现的结论是否正确？请你说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

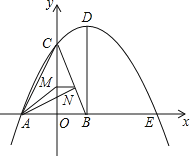
    【题目】如图，抛物线y=ax2﹣5ax+c与坐标轴分别交于点A，C，E三点，其中A（﹣3，0），C（0，4），点B在x轴上，AC=BC，过点B作BD⊥x轴交抛物线于点D，点M，N分别是线段CO，BC上的动点，且CM=BN，连接MN，AM，AN．

    （1）求抛物线的解析式及点D的坐标；

    （2）当△CMN是直角三角形时，求点M的坐标；

    （3）试求出AM+AN的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE=DF．

    （1）求证：ABCD是菱形；

    （2）若AB=5，AC=6，求ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知一次函数y=kx+4图象交直线OA于点A(1,2)，交y轴于点B，点C为坐标平面内一点.

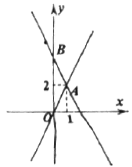
    (1)求k值;

    (2)若以O、A、B、C为顶点的四边形为菱形，则C点坐标为 ；

    (3)在直线AB上找点D，使△OAD的面积与((2)中菱形面积相等，则D点坐标为 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营，向东走为正，向西走为负，行车里程（单位：km）依先后次序记录如下：.

    （1）将最后一名乘客送到目的地，出租车离鼓楼出发点多远？在鼓楼的什么方向？

    （2）若每千米的价格为2.4元，司机一个下午的营业额是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力．2019年5月“亚洲文明对话大会”在北京成功举办，引起了世界人民的极大关注．某市一研究机构为了了解10～60岁年龄段市民对本次大会的关注程度，随机选取了100名年龄在该范围内的市民进行了调查，并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图，如下所示：

    组别

    年龄段

    频数（人数）

    第1组

    5

    第2组

    第3组

    35

    第4组

    20

    第5组

    15

    （1）请直接写出　 　，　 　，第3组人数在扇形统计图中所对应的圆心角是　 　度．

    （2）请补全上面的频数分布直方图；

    （3）假设该市现有10～60岁的市民300万人，问40～50岁年龄段的关注本次大会的人数约有多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为响应党中央号召，决定针对沿江两种主要污染源：生活污水和沿江工厂污染物排放，分别用甲方案和乙方案进行治理，若江水污染指数记为Q，沿江工厂用乙方案进行一次性治理（当年完工），从当年开始，所治理的每家工厂一年降低的Q值平均为0.3．第一年有40家工厂用乙方案治理．经过三年治理，境内沿江水质明显改善．

    （1）第一年40家工厂用乙方案治理一年降低的Q值为______；

    （2）从第二年起，每年用乙方案新治理的工厂数量比上一年都有增加，第三年新增的用乙方案．新治理的工厂数量是第二年新增的用乙方案新治理的工厂数量的1.5倍，第三年用乙方案治理所降低的Q值为57，设第二年新增的用乙方案新治理的工厂数量为m家，第三年新增的用乙方案新治理的工厂数量为n家．

    ①请列出关于m、n的方程组，并求解；

    ②该市生活污水用甲方案治理，第一年降低的Q值为20.5，从第二年起，每年所降低的Q值比上一年都增加a．若第三年用甲乙两种方案治理所降低的Q值比第二年用甲乙两种方案治理所降低的Q值大32，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】春平中学要为学校科技活动小组提供实验器材，计划购买A型、B型两种型号的放大镜．若购买8个A型放大镜和5个B型放大镜需用220元；若购买4个A型放大镜和6个B型放大镜需用152元．

    （1）求每个A型放大镜和每个B型放大镜各多少元；

    （2）春平中学决定购买A型放大镜和B型放大镜共75个，总费用不超过1180元，那么最多可以购买多少个A型放大镜？

    查看答案和解析>>

    同步练习册答案