
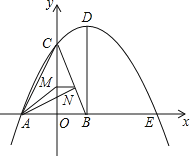
【题目】如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.
【答案】(1)抛物线解析式为y=﹣![]() x2+
x2+![]() x+4;D点坐标为(3,5);(2)M点的坐标为(0,
x+4;D点坐标为(3,5);(2)M点的坐标为(0,![]() )或(0,
)或(0,![]() );(3)AM+AN的最小值为
);(3)AM+AN的最小值为![]() .
.
【解析】(1)利用待定系数法求抛物线解析式;利用等腰三角形的性质得B(3,0),然后计算自变量为3所对应的二次函数值可得到D点坐标;
(2)利用勾股定理计算出BC=5,设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,由于∠MCN=∠OCB,根据相似三角形的判定方法,当![]() 时,△CMN∽△COB,于是有∠CMN=∠COB=90°,即
时,△CMN∽△COB,于是有∠CMN=∠COB=90°,即![]() ;当
;当![]() 时,△CMN∽△CBO,于是有∠CNM=∠COB=90°,即
时,△CMN∽△CBO,于是有∠CNM=∠COB=90°,即![]() ,然后分别求出m的值即可得到M点的坐标;
,然后分别求出m的值即可得到M点的坐标;
(3)连接DN,AD,如图,先证明△ACM≌△DBN,则AM=DN,所以AM+AN=DN+AN,利用三角形三边的关系得到DN+AN≥AD(当且仅当点A、N、D共线时取等号),然后计算出AD即可.
(1)把A(﹣3,0),C(0,4)代入y=ax2﹣5ax+c得![]() ,解得
,解得 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
∵AC=BC,CO⊥AB,
∴OB=OA=3,
∴B(3,0),
∵BD⊥x轴交抛物线于点D,
∴D点的横坐标为3,
当x=3时,y=﹣![]() ×9+
×9+![]() ×3+4=5,
×3+4=5,
∴D点坐标为(3,5);
(2)在Rt△OBC中,BC=![]() =5,
=5,
设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,
∵∠MCN=∠OCB,
∴当![]() 时,△CMN∽△COB,则∠CMN=∠COB=90°,
时,△CMN∽△COB,则∠CMN=∠COB=90°,
即![]() ,解得m=
,解得m=![]() ,此时M点坐标为(0,
,此时M点坐标为(0,![]() );
);
当![]() 时,△CMN∽△CBO,则∠CNM=∠COB=90°,
时,△CMN∽△CBO,则∠CNM=∠COB=90°,
即![]() ,解得m=
,解得m=![]() ,此时M点坐标为(0,
,此时M点坐标为(0,![]() );
);
综上所述,M点的坐标为(0,![]() )或(0,
)或(0,![]() );
);
(3)连接DN,AD,如图,
∵AC=BC,CO⊥AB,
∴OC平分∠ACB,
∴∠ACO=∠BCO,
∵BD∥OC,
∴∠BCO=∠DBC,
∵DB=BC=AC=5,CM=BN,
∴△ACM≌△DBN,
∴AM=DN,
∴AM+AN=DN+AN,
而DN+AN≥AD(当且仅当点A、N、D共线时取等号),
∴DN+AN的最小值=![]() ,
,
∴AM+AN的最小值为![]() .
.


科目:初中数学 来源: 题型:
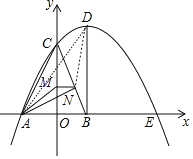
【题目】如图,动点![]() 从
从![]() 出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角(
出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角(![]() ),当点
),当点![]() 第2019次碰到矩形的边时,点
第2019次碰到矩形的边时,点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.


查看答案和解析>>
科目:初中数学 来源: 题型:
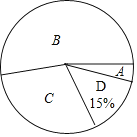
【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
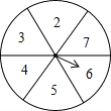
【题目】如图,现有一个均匀的转盘被平均分成六等份,分別标有2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时重转).
(1)转动转盘,转出的数字大于3的概率是______(直接填空);
(2)随机转动转盘,转盘停止后记下转出的数字,并与数字3和4分别为三条线段的长度,关于这三条线段:
①能构成三角形的概率是______(直接填空);
②能构成等腰三角形的概率是______(直接填空).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.
(1)求证:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
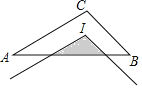
A. 4.5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C三点共线,线段AB=20 cm,BC=8 cm,点E,F分别是线段AB,BC的中点,则线段EF的长为( )
A.28 cm或12 cmB.28 cmC.14 cmD.14cm或6 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com