
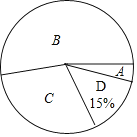
【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
【答案】(1)51,30;(2)C等级所对应扇形的圆心角度数为108°.(3)P(选中1名男生和1名女生)=![]() .
.
【解析】(1)由A的人数和其所占的百分比即可求出总人数,由此即可解决问题;
(2)由总人数求出C等级人数,根据其占被调查人数的百分比可求出其所对应扇形的圆心角的度数;
(3)列表得出所有等可能的情况数,找出刚好抽到一男一女的情况数,即可求出所求的概率.
(1)参加本次比赛的学生有:4÷0.04=100(人),
m=0.51×100=51(人),
D组人数=100×15%=15(人),
n=100﹣4﹣51﹣15=30(人)
故答案为51,30;
(2)B等级的学生共有:50﹣4﹣20﹣8﹣2=16(人),
∴所占的百分比为:16÷50=32%,
∴C等级所对应扇形的圆心角度数为:360°×30%=108°;
(3)列表如下:
男 | 女1 | 女2 | 女3 | |
男 | ﹣﹣﹣ | (女,男) | (女,男) | (女,男) |
女1 | (男,女) | ﹣﹣﹣ | (女,女) | (女,女) |
女2 | (男,女) | (女,女) | ﹣﹣﹣ | (女,女) |
女3 | (男,女) | (女,女) | (女,女) | ﹣﹣﹣ |
∵共有12种等可能的结果,选中1名男生和1名女生结果的有6种.
∴P(选中1名男生和1名女生)=![]() .
.


科目:初中数学 来源: 题型:
【题目】若![]() 互为相反数,
互为相反数,![]() 互为倒数,且
互为倒数,且![]() 的立方等于它本身.
的立方等于它本身.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 试讨论:当
试讨论:当![]() 为有理数时,
为有理数时,![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
![]() 若
若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
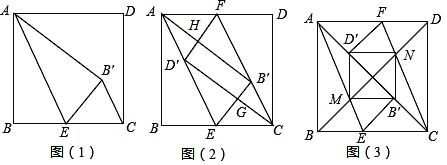
【题目】综合与实践:折纸中的数学
问题情境:数学活动课上,老师让同学们折叠正方形纸片ABCD进行探究活动,兴趣小组的同学经过动手操作探究,提出了如下两个问题:
问题1:如图(1),若点E为BC的中点,设AE将正方形纸片ABCD折叠,点B的对应点为B′,连接B′C,求证:B′C∥AE.
问题2:如图(2),若点E,点F分别为边BC,边AD的中点,沿AE、CF将正方形纸片ABCD折叠,点B的对应点为B′,点D的对应点D′,D′F与AB′交于点H,B′E与CD′交于点G,求证:四边形D′GB′H为矩形.
(1)解决问题:请你对兴趣小组提出的两个问题进行证明.
(2)拓展探究:解决完兴趣小组提出的两个问题后,实践小组的同学们进行如下实践操作:如图(3),点E,点F分别为BC、AD上的点,将正方形纸片沿AE、CF折叠,使得点B落在对角线上的点B′处,点D落在对角线AC上的点D′处,AE与对角线BD的交点为M,CF与对角线BD的交点为N,分别连接MB′,B′N,D′N,D′M.他们认为四边形MB′ND′为正方形.
实践小组的同学们发现的结论是否正确?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列已知条件,分别指出两个图形中的等腰三角形,并利用第一个图证明结论。
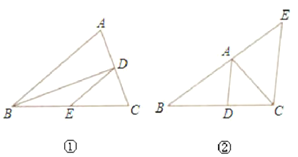
(1)如图①,BD平分∠ABC,DE//AB
(2) 如图②,AD平分∠BAC , EC//AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,
,![]() 是数轴上一点,且
是数轴上一点,且![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,设运动时间为
个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
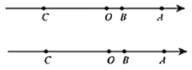
(1)数轴上点![]() 表示的数为 ,并用含
表示的数为 ,并用含![]() 的代数式表示点
的代数式表示点![]() 所表示的数为 ;
所表示的数为 ;
(2)设![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由,若不变,求线段
的长度是否发生变化?若变化,请说明理由,若不变,求线段![]() 的长度;
的长度;
(3)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,动点
个单位长度的速度沿数轴向左匀速运动,动点![]() 从点
从点![]() 出发,以点每秒
出发,以点每秒个单位长度沿数轴向左匀速运动,若
![]() 三点同时出发,在运动过程中,
三点同时出发,在运动过程中,![]() 到
到![]() 的距离,
的距离,![]() 到
到![]() 距离中,是否会有这两段距离相等的时候?若有,请求出此时的值;若没有,请说明理由.
距离中,是否会有这两段距离相等的时候?若有,请求出此时的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
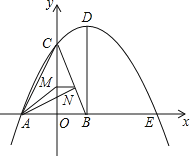
【题目】如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为响应党中央号召,决定针对沿江两种主要污染源:生活污水和沿江工厂污染物排放,分别用甲方案和乙方案进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值平均为0.3.第一年有40家工厂用乙方案治理.经过三年治理,境内沿江水质明显改善.
(1)第一年40家工厂用乙方案治理一年降低的Q值为______;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都有增加,第三年新增的用乙方案.新治理的工厂数量是第二年新增的用乙方案新治理的工厂数量的1.5倍,第三年用乙方案治理所降低的Q值为57,设第二年新增的用乙方案新治理的工厂数量为m家,第三年新增的用乙方案新治理的工厂数量为n家.
①请列出关于m、n的方程组,并求解;
②该市生活污水用甲方案治理,第一年降低的Q值为20.5,从第二年起,每年所降低的Q值比上一年都增加a.若第三年用甲乙两种方案治理所降低的Q值比第二年用甲乙两种方案治理所降低的Q值大32,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com