
【题目】某校为了了解七年级![]() 名学生其中数学考试情况,从中抽取了
名学生其中数学考试情况,从中抽取了![]() 名学生的数学成绩进行了统计,下面
名学生的数学成绩进行了统计,下面![]() 个判断中正确的有( )个.
个判断中正确的有( )个.
①这种调查的方式是抽样调查;②![]() 名学生是总体;③每名学生的数学成绩是个体;④
名学生是总体;③每名学生的数学成绩是个体;④![]() 名学生是总体的一个样本;⑤样本容量是
名学生是总体的一个样本;⑤样本容量是![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),
则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(Ⅰ)点P(﹣2,3)的“3属派生点”P′的坐标为 ;
(Ⅱ)若点P的“5属派生点”P′的坐标为(3,﹣9),求点P的坐标;
(Ⅲ)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
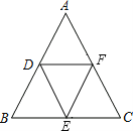
【题目】如图,在△ABC中,∠B=∠C=∠DEF,点D、E、F分别在AB、AC上,且BD=CE.求证:DE=EF.
证明:(请将下面的证明过程补充完整)
∵∠B+∠BDE+∠BED=180°(______)
∠DEF+∠FEC+∠BED=180°(______)
∠B=∠DEF(已知)
∴∠BDE=∠FEC(______)
在△BDE和△CEF中
∠B=∠C(已知)
BD=CE(______)
∠BDE=∠FEC(______)
∴△BDE≌△CEF(______)(用字母表示)
∴DE=EF(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+4图象交直线OA于点A(1,2),交y轴于点B,点C为坐标平面内一点.
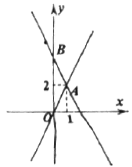
(1)求k值;
(2)若以O、A、B、C为顶点的四边形为菱形,则C点坐标为 ;
(3)在直线AB上找点D,使△OAD的面积与((2)中菱形面积相等,则D点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲乙两家商店出售两种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠,该班现需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)若购买的乒乓球为![]() 盒,请分别用代数式表示在两家店购买这些乒乓球和乒乓球拍时应该支付的费用;
盒,请分别用代数式表示在两家店购买这些乒乓球和乒乓球拍时应该支付的费用;
(2)当购买15盒、30盒乒乓球时,请你去办这件事,你打算去哪家商店购买,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |

(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入它所属于的集合的括号内.
9,![]() ,+4.3,|﹣0.5|,﹣(+7),18%,(﹣13)4,﹣6,0.
,+4.3,|﹣0.5|,﹣(+7),18%,(﹣13)4,﹣6,0.
正分数集合{_________}
负分数集合{_________}
负整数集合{__________}
非负整数集合{________}.
查看答案和解析>>
科目:初中数学 来源: 题型:
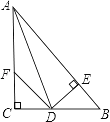
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com