
【题目】如图1,将正方形![]() 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中![]() 边在
边在![]() 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线![]() 沿
沿![]() 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形![]() 的边所截得的线段长为
的边所截得的线段长为![]() ,平移的时间为
,平移的时间为![]() (秒),
(秒),![]() 与
与![]() 的函数图象如图2所示,则图1中的点
的函数图象如图2所示,则图1中的点![]() 的坐标为__________,图2中
的坐标为__________,图2中![]() 的值为__________.
的值为__________.


![]()
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() .把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是__________.
.把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国庆”期间,某电影院装修后重新开业,试营业期间统计发现,影院每天售出的电影票张数y(张)与电影票售价![]() (元/张)之间满足一次函数关系:
(元/张)之间满足一次函数关系: ![]() ,
, ![]() 是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入
是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入![]() 运营成本).
运营成本).
(1)试求w与![]() 之间的函数关系式;
之间的函数关系式;
(2)影院将电影票售价定为多少时,每天获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴,y轴相交于A,B两点,0为坐标原点,A点的坐标为(4,0)
分别与x轴,y轴相交于A,B两点,0为坐标原点,A点的坐标为(4,0)
(1)求k的值;
(2)过线段AB上一点P(不与端点重合)作x轴,y轴的垂线,乖足分别为M,N.当长方形PMON的周长是10时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF//BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.
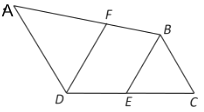
解: 因为DF平分∠CDA,(已知)
所以∠FDC=![]() ∠_________.(____________________)
∠_________.(____________________)
因为∠CDA=120°,(已知)所以∠FDC=______°.
因为DF//BE,(已知)
所以∠FDC=∠_________=60°.(____________________________________)
又因为EC=EB,(已知)
所以△BCE为等边三角形.(________________________________________)
因为△BCE的周长为18cm,(已知) 所以BE=EC=BC=6 cm.
因为点E是DC的中点,(已知) 所以DC=2EC=12 cm .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com