练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直线分别与x轴，y轴相交于A，B两点，0为坐标原点，A点的坐标为(4，0)

    （1）求k的值；

    （2）过线段AB上一点P(不与端点重合)作x轴，y轴的垂线，乖足分别为M，N.当长方形PMON的周长是10时，求点P的坐标.

    【答案】（1）k=﹣2；（2）点P的坐标为（3，2）.

    【解析】试题分析：（1）因为直线分别与轴， 轴相交于两点，O为坐标原点，A点的坐标为即直线经过所以 解之即可；
    （2）因为四边形是矩形，点P在直线上，设 则 而 由此即可得到关于的方程，解方程即可求得．

    试题解析：(1)∵直线y=kx+8经过A(4,0)，

    ∴0=4k+8，

    ∴k=2.

    (2)∵点P在直线y=2x+8上,设P(t,2t+8)，

    ∴PN=t，PM=2t+8，

    ∵四边形PNOM是矩形，

    解得

    ∴点P的坐标为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

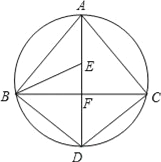
    【题目】如图，AD为△ABC外接圆的直径，AD⊥BC，垂足为点F，∠ABC的平分线交AD于点E，连接BD，CD．

    （1）求证：BD=CD；

    （2）请判断B，E，C三点是否在以D为圆心，以DB为半径的圆上？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：

    （1）如果∠1＝∠B，那么_______∥_______，根据是__________________________；

    （2）如果∠3＝∠D，那么_______∥_______，根据是__________________________；

    （3）如果要使BE∥DF，必须∠1＝∠_______，根据是_________________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

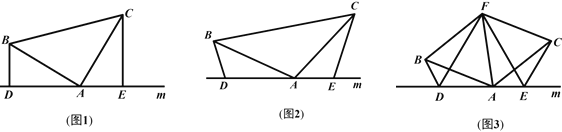
    【题目】（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE＝BD+CE．

    （2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？若成立，请给出证明；若不成立，请说明理由．

    （3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点

    互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：（x+2）（x2﹣2ax+3）中不含x2项，a＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知函数的图象与x轴、y轴分别交于点A、B，与函数图象交于点M，点M的横坐标为2，在x轴上有点P(a，0)（其中a>2)，过点P作x轴的垂线，分别交函数和的图象于点C、D.

    （1）求点A的坐标：

    （2）若OB=CD，求a的值

    （3）在（2）条件下若以0D线段为边，作正方形0DEF，求直线EF的表达式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列语句中，是真命题的是( )

    A.相等的角是对顶角

    B.同旁内角互补

    C.过一点不只有一条直线与已知直线垂直

    D.对于直线 a、b、c，如果 b∥a，c∥a，那么 b∥c

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平面内点M（x，y），若x，y满足下列条件，请说出点M的位置．

    （1）xy＜0；（2）x+y=0；（3）=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

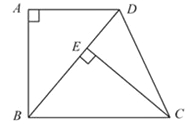
    【题目】如图，已知四边形ABCD是梯形，AD∥BC，∠A＝90°，BC＝BD，CE⊥BD，垂足为E．

    (1)求证：△ABD≌△ECB；

    (2)若∠DBC＝50°，求∠DCE的度数．

    查看答案和解析>>

    同步练习册答案