
【题目】如图,将一张矩形纸片沿着AE折叠后,点D恰好与BC边上的点F重合,已知AB=6cm,BC=10cm,则EC的长度为_____cm.

【答案】3.
【解析】
先根据翻折变换的性质得出Rt△ADE≌Rt△AEF,再先设EC的长为x,则AF=10cm,EF=DE=(8﹣x)cm,在Rt△ABF中由勾股定理得:AB2+BF2=AF2,已知AB、AF的长可求出BF的长,又CF=BC﹣BF=10﹣BF,在Rt△ECF中由勾股定理可得:EF2=EC2+CF2,即:(8﹣x)2=x2+(10﹣BF)2,将求出的BF的值代入该方程求出x的值,即求出了EC的长.
解:∵△AEF由△ADE翻折而成,
∴Rt△ADE≌Rt△AEF,
∴∠AFE=90°,AD=AF=10cm,EF=DE,
设EC=xcm,则DE=EF=CD﹣EC=(8﹣x)cm,
在Rt△ABF中由勾股定理得:AB2+BF2=AF2,
即82+BF2=102,
∴BF=6cm,
∴CF=BC﹣BF=10﹣6=4(cm),
在Rt△ECF中由勾股定理可得:EF2=EC2+CF2,
即(8﹣x)2=x2+42,
∴64﹣16x+x2=x2+16,
∴x=3(cm),即EC=3cm,
故答案为:3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将正方形![]() 置于平面直角坐标系中,其中
置于平面直角坐标系中,其中![]() 边在
边在![]() 轴上,其余各边均与坐标轴平行.直线
轴上,其余各边均与坐标轴平行.直线![]() 沿
沿![]() 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形
轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形![]() 的边所截得的线段长为
的边所截得的线段长为![]() ,平移的时间为
,平移的时间为![]() (秒),
(秒),![]() 与
与![]() 的函数图象如图2所示,则图1中的点
的函数图象如图2所示,则图1中的点![]() 的坐标为__________,图2中
的坐标为__________,图2中![]() 的值为__________.
的值为__________.


![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
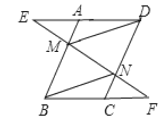
【题目】已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E、F,且AE=CF.
(1) 求证:△AEM≌△CFN.
(2) 求证:四边形BNDM是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 交y轴于点A,交直线x=6于点B.
交y轴于点A,交直线x=6于点B.
(1)填空:抛物线的对称轴为x=_________,点B的纵坐标为__________(用含a的代数式表示);
(2)若直线AB与x轴正方向所夹的角为45°时,抛物线在x轴上方,求![]() 的值;
的值;
(3)记抛物线在A、B之间的部分为图像G(包含A、B两点),若对于图像G上任意一点![]() ,总有
,总有![]() ≤3,求a的取值范围.
≤3,求a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=x-3交x轴于点B,交y轴于点C,抛物线经过点A(-1,0),B,C三点,点F在y轴负半轴上,OF=OA.
(1)求抛物线的解析式;
(2)在第一象限的抛物线上存在一点P,满足S△ABC=S△PBC,请求出点P的坐标;
(3)点D是直线BC的下方的抛物线上的一个动点,过D点作DE∥y轴,交直线BC于点E,①当四边形CDEF为平行四边形时,求D点的坐标;
②是否存在点D,使CE与DF互相垂直平分?若存在,请求出点D的坐标;若不存在,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com