Question

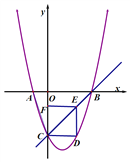
【题目】如图，在直角坐标系中，直线y=x-3交x轴于点B，交y轴于点C，抛物线经过点A(-1，0)，B，C三点,点F在y轴负半轴上，OF=OA.

(1)求抛物线的解析式；

(2)在第一象限的抛物线上存在一点P，满足S△ABC=S△PBC，请求出点P的坐标；

(3)点D是直线BC的下方的抛物线上的一个动点，过D点作DE∥y轴，交直线BC于点E，①当四边形CDEF为平行四边形时，求D点的坐标；

②是否存在点D，使CE与DF互相垂直平分？若存在，请求出点D的坐标；若不存在，请说明理由．

Answer 1

【答案】(1) y=(x+1)(x-3)=x2-2x-3;

(2) P（4,5）

（3）①D(1,-4)或（2,-3），

②存在D（2,-3），使CE与DF互相垂直平分,理由见解析.

【解析】试题分析：（1）先根据直线解析式确定出B 、C的坐标，然后利用待定系数法即可得；

（2）过点A作AP∥BC，交抛物线于P点，P点满足S△ABC=S△PBC，求出AP的解析式，然后与抛物线的解析式联立组成方程组，求解即可得；

（3）根据点E在BC上，点D在抛物线上，设D（x，x2-2x-3），E(x，x-3)，则DE= -x2+3x，

①四边形CDEF为平行四边形可知DE=CF=2，解方程即可得；

②当四边形CDEF为正方形时，才有CE与DF互相垂直平分，据此即可得.

试题解析：(1)由直线y=x-3与坐标轴交于B、C两点，则有B（3，0），C（0，-3），

由题意设抛物线得解析式为y=a(x+1)(x-3)，

将C点坐标代入，得-3=-3a，

解得，a=1，

∴抛物线解析式为y=(x+1)(x-3)=x2-2x-3；

(2)过点A作AP∥BC，交抛物线于P点，P点满足S△ABC=S△PBC，

设直线AP的解析式为y=x+b，则0=-1+b，∴b=1，

∴直线AP的解析式为y=x+1，

由解得，

∴P（4，5）；

（3）易得F（0，-1），CF=2，

设D（x，x2-2x-3），E(x，x-3)，则DE=x-3-(x2-2x-3)=-x2+3x，

①令-x2+3x=2，解得x3=1，x4=2，

D(1，-4)或（2，-3），

②存在，

当D（2，-3）时E（2，-1），EF⊥CF，且EF=CF，

∴平行四边形CDEF为正方形，

∴CE与DF互相垂直平分。

∴存在D（2，-3），使CE与DF互相垂直平分.