
【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).

(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
【答案】(1)y=﹣![]() (x﹣2)2(2)证明见解析(3)
(x﹣2)2(2)证明见解析(3)![]() (4)
(4)![]()
【解析】试题分析:(1)用待定系数法求,即可;
(2)由对称的特点得出∠N1BN2=2∠DBC结合菱形的性质即可;
(3)先判定出,当BN⊥CD时,BN最短,再利用△ABC∽△N1BN2得到比例式,求解,即可;
(4)先建立PE=![]() m2﹣
m2﹣![]() m+2函数解析式,根据抛物线的特点确定出最小值.
m+2函数解析式,根据抛物线的特点确定出最小值.
试题解析:(1)由已知,设抛物线解析式为y=a(x﹣2)2
把D(0,﹣1)代入,得a=﹣![]()
∴y=﹣![]() (x﹣2)2
(x﹣2)2
(2)如图1,连结BN.
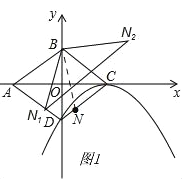
∵N1,N2是N的对称点
∴BN1=BN2=BN,∠N1BD=∠NBD,∠NBC=∠N2BC
∴∠N1BN2=2∠DBC
∵四边形ABCD是菱形
∴AB=BC,∠ABC=2∠DBC
∴∠ABC=∠N1BN2, ![]()
∴△ABC∽△N1BN2
(3)∵点N是CD上的动点,
∴点到直线的距离,垂线段最短,
∴当BN⊥CD时,BN最短.
∵C(2,0),D(0,﹣1)
∴CD=![]() ,
,
∴BNmin=![]() ,
,
∴BN1min=BNmin=![]() ,
,
∵△ABC∽△N1BN2
∴![]() ,
,
N1N2min=![]() ,
,
(4)如图2,
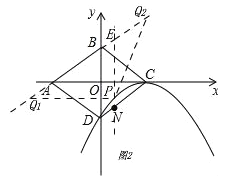
过点P作PE⊥x轴,交AB于点E.
∵∠PQA=∠BAC
∴PQ1∥AC
∵菱形ABCD中,C(2,0),D(0,﹣1)
∴A(﹣2,0),B(0,1)
∴lAB:Y=![]() x+1
x+1
不妨设P(m,﹣![]() (m﹣2)2),则E(m,
(m﹣2)2),则E(m, ![]() m+1)
m+1)
∴PE=![]() m2﹣
m2﹣![]() m+2
m+2
∴当m=1时, ![]()
此时,PQ1最小,最小值为![]() =
=![]() ,
,
∴PQ1=PQ2=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(3,1),将A点沿与x轴平行的直线向左平移,使点A的落在直线y=﹣3x﹣2上,则点A平移的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2-2(3x-2)+(x+1)=0的一般形式是( )
A.x2-5x+5=0 B.x2+5x-5=0 C.x2+5x+5=0 D.x2+5=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.
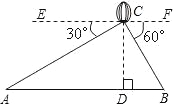
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x,y)在第二象限|x+1|=2,|y﹣2|=3,则点P的坐标为( )
A. (﹣3,5)B. (1,﹣1)C. (﹣3,﹣1)D. (1,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在百货商场购进了A、B两种品牌的篮球,购买A品牌蓝球花费了2400元,购买B品牌蓝球花费了1950元,且购买A品牌蓝球数量是购买B品牌蓝球数量的2倍,已知购买一个B品牌蓝球比购买一个A品牌蓝球多花50元.
(1)求购买一个A品牌、一个B品牌的蓝球各需多少元?
(2)该学校决定再次购进A、B两种品牌蓝球共30个,恰逢百货商场对两种品牌蓝球的售价进行调整,A品牌蓝球售价比第一次购买时提高了10%,B品牌蓝球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌蓝球的总费用不超过3200元,那么该学校此次最多可购买多少个B品牌蓝球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com