
����Ŀ��������������ѧϰ�������������ĵĸ�����ǿ��������ĵĶ��壺�������ε��������������ȵĵ㣬�����������ε����ģ���ش�������������⣺

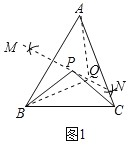
��1����ͼ1����PB��PC�����PΪ��ABC�����ģ���������֪�������������������������������ܷ��ó߹���������һ������Q�أ��볢����ɣ�
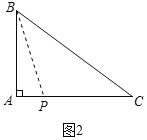
��2����ͼ2����֪��ABCΪֱ�������Σ�б��BC��5��AB��3������P��AC���ϣ���̽��PA�ij���
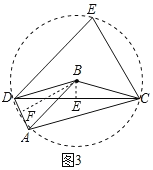
��3����ͼ3����B������EDC������ADC�����ģ�BD��BA��BC��2AD��BD��AC��CD��![]() ����AD��ֵ��
����AD��ֵ��
���𰸡���1�����ó߹���������һ������Q����ͼ1��ʾ����QΪ��ABC�����ģ���2������P��AC���ϣ�PA�ij�Ϊ![]() ��2����3��AD��
��2����3��AD��![]() ��
��
��������
��1����AB�Ĵ�ֱƽ����MN����MN��ȡ��Q���ɣ�
��2������BP���ɹ��ɶ����ó�AC=4��������������ۣ���ֱ�������ε����ʼ��ɵó��𰸣�
��3����BD=BA=BC���ó���BAC=��BCA����D��A��C����BΪԲ�ģ�AB��Ϊ�뾶��Բ�ϣ���Բ�ܽǶ����ó���ABD=2��ACD����BE��CD��E��BF��AD��F���ɴ��������ó�DE=CE![]() CD
CD![]() ��DF=AF
��DF=AF![]() AD����ABD=2��DBF����BEC=��DFB=90�㣬֤����BDF�ա�CBE���ó�DF=BE����DF=x����BE=x��AD=2x��BD=2AD=4x����Rt��BDE�У��ɹ��ɶ����ó����̣��ⷽ�̼��ɣ�
AD����ABD=2��DBF����BEC=��DFB=90�㣬֤����BDF�ա�CBE���ó�DF=BE����DF=x����BE=x��AD=2x��BD=2AD=4x����Rt��BDE�У��ɹ��ɶ����ó����̣��ⷽ�̼��ɣ�
��1�����ó߹���������һ������Q��
��AB�Ĵ�ֱƽ����MN����MN��ȡ��Q����ͼ1��ʾ��
��QA=QB����QΪ��ABC�����ģ�
��2������BP����ͼ2��ʾ��
�ߡ�ABCΪֱ�������Σ�б��BC=5��AB=3��
��AC![]() 4��
4��
������P��AC���ϣ�
�ٵ�PB=PCʱ��
��PB=x����PC=x��PA=4��x��
��Rt��ABP�У��ɹ��ɶ����ã�32+��4��x��2=x2��
��ã�x![]() ��
��
��PA=4![]() ��
��
�ڵ�PA=PCʱ��PA![]() AC=2��
AC=2��
�۵�PA=PBʱ��
�ߡ�ABC��ֱ�������Σ������������ڣ�
��������������P��AC���ϣ�PA�ij�Ϊ![]() ��2��
��2��
��3����BD=BA=BC�����BAC=��BCA����D��A��C����BΪԲ�ģ�AB��Ϊ�뾶��Բ�ϣ���ͼ3��ʾ�����ABD=2��ACD��
��BE��CD��E��BF��AD��F��
��DE=CE![]() CD
CD![]() ��DF=AF
��DF=AF![]() AD��
AD��
��ABD=2��DBF����BEC=��DFB=90�㣮
��BD��AC��
���ABD=��BAC=��BCA=2��ACD=2��DBF=2��BCE��
���DBF=��BCE��
�ڡ�BDF�͡�CBE�У���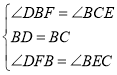 ��
��
���BDF�ա�CBE��ASA������DF=BE��
��DF=x����BE=x��AD=2x��BD=2AD=4x��
��Rt��BDE�У��ɹ��ɶ����ã�x2+��![]() ��2=��4x��2��
��2=��4x��2��
��ã�x![]() ����AD=2x
����AD=2x![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��F�ֱ��DZ�AD��BC���е㣬����DF������E��EH��DF������ΪH��EH���ӳ��߽�DC�ڵ�G��
��1������DG��CF��������ϵ����֤����Ľ��ۣ�
��2������H��MN��CD���ֱ�AD��BC�ڵ�M��N����������ABCD�ı߳�Ϊ10����P��MN��һ�㣬���PDC�ܳ�����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() ���˶���
���˶���![]() ����
����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ����
����![]() ��
��![]() ���߶�
���߶�![]() ��
��![]() .
.

��1����![]() ʱ��
ʱ��![]() ______________
______________![]() ����
����![]() ��
��![]() ��
��![]() �˶�ʱ��
�˶�ʱ��![]() ��____________��������������С������
��____________��������������������
��2����![]() ʱ����֤��
ʱ����֤��![]() ����˵�����ɣ�
����˵�����ɣ�
��3���ڵ�![]() ���˶������У�
���˶������У�![]() ����״Ҳ�ڸı䣬�жϵ�
����״Ҳ�ڸı䣬�жϵ�![]() ���ڶ��ٶ�ʱ��
���ڶ��ٶ�ʱ��![]() �ǵ���������.
�ǵ���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�MΪBC��һ�㣬F��AM���е㣬EF��AM������ΪF����AD���ӳ����ڵ�E����DC�ڵ�N��

��1����֤����ABM�ס�EFA��
��2����AB=12��BM=5����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
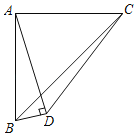
����Ŀ����ͼ������ֱ��������ABC��ֱ�DZߵij���a��AD��BD����AD��3BD������BCD�������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�г�;����վÿ��6��30��7��30����ij�ص������Ʊ����ͬ�����������ʳ̶Ȳ�ͬ.С�ź�С������������һʱ�γ˳�ȥ���أ�����֪��������������˳�����˲��ò�ͬ�ij˳�������С��������ξ������������ĵ�һ��������С�������ȹ۲���ϳ�������һ��������ʱ�������ϳ���������ϸ�۲쳵������״��.���ڶ�������״���ȵ�һ�����ã������ϵڶ����������ڶ����������һ�����������ϵ�������.�����������������ʳ̶ȷ�Ϊ�š��С������ȣ�����˼�����ش��������⣺
(1)�����������ֵ��Ⱥ�˳�����ļ��ֿ��ܣ�
(2)���б��������ַ��������ŵȳ��Ŀ����Դ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��CAD����CEB���ǵȱ������Σ�BD��EA���ӳ����ཻ�ڵ�F��
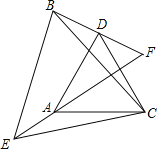
��1����֤����ACE�ա�DCB��
��2�����F�Ķ�����
��3����AD��BD����ֱ��д���߶�EF���߶�BD��DF֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ڡ����ҹ��Ĵ�ͳ�ѽڣ���������гԡ����ӡ���ϰ�ף�����ijʳƷ��Ϊ�˽������ȥ�������Ϻõ������ա���ɳ���ա��������ա��������գ����·ֱ���A��B��C��D��ʾ�������ֲ�ͬ��ζ���ӵ�ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ���в���������
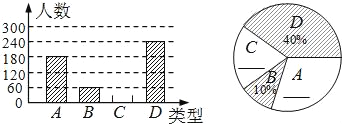
�����������Ϣ�ش�
��1�����βμӳ�������ľ����ж����ˣ�
��2����������������ͼ����������
��3��������ͳ��ͼ��C����Բ�ĽǵĶ�����
��4������������ȫ��ͬ��A��B��C��D�ո�һ���������С���������������б�����״ͼ�ķ����������ڶ����Ե���ǡ����C�յĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
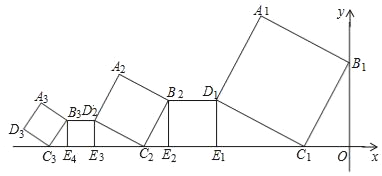
����Ŀ��һ�������ΰ���ͼ��ʾ�ķ�ʽ���ã����ж���B1��y���ϣ�����C1��E1��E2��C2��E3��E4��C3������x���ϣ���֪������A1B1C1D1�Ķ���C1�������ǣ���![]() ��0������B1C1O=60�㣬B1C1��B2C2��B3C3������������A2018B2018C2018D2018�Ķ���D2018��������_____��
��0������B1C1O=60�㣬B1C1��B2C2��B3C3������������A2018B2018C2018D2018�Ķ���D2018��������_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com