
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD =∠BCE = 90°,点M为AN的中点,过点E与AD平行的直线交射线AM于点N。
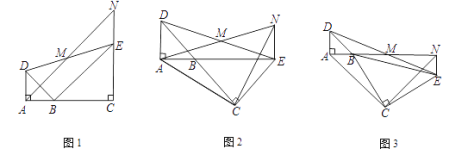
(1)当A,B,C三点在同一直线上时(如图1),求证:AD=NE ;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由。
【答案】(1)见解析;(2)见解析;(3)成立,证明见解析
【解析】
(1)由EN∥AD,点M为AN的中点,利用AAS证得△ADM≌△NEM,从而得到结论;
(2)易证AB=DA=NE,∠ABC=∠NEC=135°,从而可以证到△ABC≌△NEC,进而可以证到AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形;
(3)借鉴(2)中的解题经验可得AB=DA=NE,∠ABC=∠NEC=180°-∠CBN,从而可以证到△ABC≌△NEC,进而可以证到AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形.
(1)如图1,
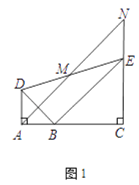
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为AN的中点,
∴AM=MN.
在△ADM和△NEM中,
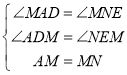
∴△ADM≌△NEM(AAS).
∴AD=NE;
(2)如图2,
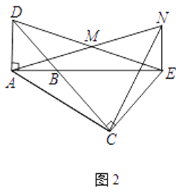
∵![]() BAD和△BCE均为等腰直角三角形,
BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD∥NE,∴∠DAE+∠NEA=180°.
∵∠DAE=90°,∴∠NEA=90°.
∴∠NEC=135°.
∵A,B,E三点在同一直线上,
∴∠ABC=180°﹣∠CBE=135°.
∴∠ABC=∠NEC.
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为AN的中点,
∴AM=MN.
在△ADM和△NEM中,
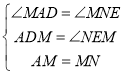
∴△ADM≌△NEM(AAS).
∴AD=NE.
又∵AD=AB,∴AB=NE.
在△ABC和△NEC中,
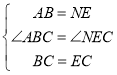
∴△ABC≌△NEC(SAS).
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
(3)△ACN仍为等腰直角三角形.
如图3,
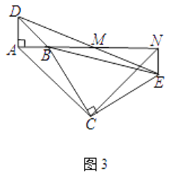
此时A、B、N三点在同一条直线上.
∵AD∥EN,∠DAB=90°,∴∠ENA=∠DAN=90°.
∵∠BCE=90°,∴∠CBN+∠CEN=360°﹣90°﹣90°=180°.
∵A、B、N三点在同一条直线上,∴∠ABC+∠CBN=180°.
∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),AD=NE.
又∵AD=AB,∴AB=NE.
在△ABC和△NEC中,
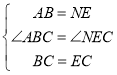
∴△ABC≌△NEC(SAS).
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
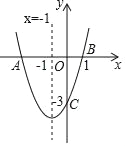
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
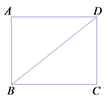
【题目】如图,在矩形ABCD中,对角线BD的长为1,点P是线段BD上的一点,联结CP,将△BCP沿着直线CP翻折,若点B落在边AD上的点E处,且EP//AB,则AB的长等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx经过点A(﹣1,![]() )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的
轴的
正半轴上,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 的坐标为
的坐标为![]() .
.

![]() 求
求![]() 的值.
的值.
![]() 若将菱形
若将菱形![]() 向右平移,使点
向右平移,使点![]() 落在反比例函数
落在反比例函数![]() 的图象上,求菱形
的图象上,求菱形![]() 平移的距离.
平移的距离.
![]() 怎样平移可以使点
怎样平移可以使点![]() 、
、![]() 同时落在第一象限的曲线上?
同时落在第一象限的曲线上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论;
(2)过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com