
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,双曲线
,双曲线![]() 经过点
经过点![]() .
.

(1)求直线![]() 和双曲线
和双曲线![]() 的解析式.
的解析式.
(2)平移直线![]() ,使它与双曲线
,使它与双曲线![]() 有唯一公共点
有唯一公共点![]() 时,求点
时,求点![]() 的坐标.
的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(问题提出):有同样大小正方形256个,拼成如图1所示的![]() 的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?
的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?

(问题探究):我们先考虑以下简单的情况:一条直线穿越一个正方形的情况.(如图2)
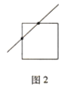
从图中我们可以看出,当一条直线穿过一个小正方形时,这条直线最多与正方形上、下、左、右四条边中的两个边相交,所以当一条直线穿过一个小正方形时,这条直线会与其中某两条边产生两个交点,并且以两个交点为顶点的线段会全部落在小正方形内.
这就启发我们:为了求出直线![]() 最多穿过多少个小正方形,我们可以转而去考虑当直线
最多穿过多少个小正方形,我们可以转而去考虑当直线![]() 穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
再让我们来考虑![]() 正方形的情况(如图3):
正方形的情况(如图3):
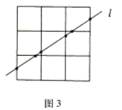
为了让直线穿越更多的小正方形,我们不妨假设直线![]() 右上方至左下方穿过一个
右上方至左下方穿过一个![]() 的正方形,我们从两个方向来分析直线
的正方形,我们从两个方向来分析直线![]() 穿过
穿过![]() 正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线
正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线![]() 最多可穿过
最多可穿过![]() 的大正方形中的六条线段,从而直线
的大正方形中的六条线段,从而直线![]() 上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线
上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线![]() 最多能经过5个小正方形.
最多能经过5个小正方形.
(问题解决):
(1)有同样大小的小正方形16个,拼成如图4所示的![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.

(2)有同样大小的小正方形256个,拼成![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
(3)如果用一条直线穿过![]() 的大正方形的话,最多可以穿过___________个小正方形.
的大正方形的话,最多可以穿过___________个小正方形.
(问题拓展):
(4)如果用一条直线穿过![]() 的大长方形的话(如图5),最多可以穿过个___________小正方形.
的大长方形的话(如图5),最多可以穿过个___________小正方形.

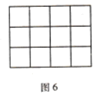
(5)如果用一条直线穿过![]() 的大长方形的话(如图6),最多可以穿过___________个小正方形.
的大长方形的话(如图6),最多可以穿过___________个小正方形.
(6)如果用一条直线穿过![]() 的大长方形的话,最多可以穿过________个小正方形.
的大长方形的话,最多可以穿过________个小正方形.
(类比探究):
由二维的平面我们可以联想到三维的立体空间,平面中的正方形中四条边可联想到正方体中的正方形的六个面,类比上面问题解决的方法解决如下问题:
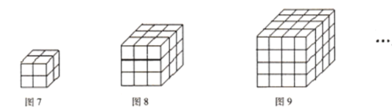
(7)如图7有同样大小的小正方体8个,拼成如图所示的![]() 的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
(8)如果用一条直线穿过![]() 的大正方体的话,最多可以穿过_________个小正方体.
的大正方体的话,最多可以穿过_________个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
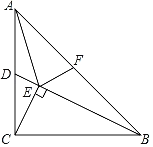
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=2,D是边AC的中点,CE⊥BD于E.若F是边AB上的点,且使△AEF为等腰三角形,则AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为![]() ,投人市场销售时,调査市场行情,发现该蜜柚销售不会亏本,且每天销售量
,投人市场销售时,调査市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (单位:千克)与销售单价
(单位:千克)与销售单价![]() (单位:
(单位: ![]() )之间的函数关系如图
)之间的函数关系如图
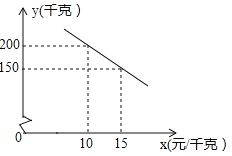
(1)求![]() 与
与![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大,最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年新型冠状病毒肺炎(![]() ,简称为新冠肺炎)疫情在全球蔓延,我们国家坚决打赢这场无硝烟的人民战争,我市各单位为同学们的返校复学采取了一系列前所未有的举措.复课返校后,为了拉大学生锻炼的间距,某学校决定增购适合独立训练的两种体育器材:跳绳和毽子,原来购进
,简称为新冠肺炎)疫情在全球蔓延,我们国家坚决打赢这场无硝烟的人民战争,我市各单位为同学们的返校复学采取了一系列前所未有的举措.复课返校后,为了拉大学生锻炼的间距,某学校决定增购适合独立训练的两种体育器材:跳绳和毽子,原来购进![]() 根跳绳和
根跳绳和![]() 个毽子共需
个毽子共需![]() 元;购进
元;购进![]() 根跳绳和
根跳绳和![]() 个键子共需
个键子共需![]() 元.
元.
(1)求跳绳和毽子的售价原来分别是多少元?
(2)学校计划购买跳绳和毽子两种器材共![]() 个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的
个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的![]() 倍,跳绳的数量不多于
倍,跳绳的数量不多于![]() 根,请你求出学校花钱最少的购买方案.
根,请你求出学校花钱最少的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小花在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小花身高1.5米,当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是![]() 年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
甲厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
乙厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
丙厂:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
请回答下面问题:
(1)填空:
平均数 | 众数 | 中位数 | |
甲厂 | _____ |
|
|
乙厂 |
| ______ |
|
丙厂 |
|
| ______ |
(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数;
(3)如果你是顾客,你会买三家中哪一家的电子产品?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
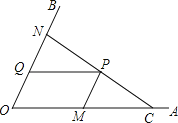
(1)若∠AOB=45°,OM=4,OQ=![]() ,求证:CN⊥OB;
,求证:CN⊥OB;
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由;
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由;
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,正方形OABC如图放置,反比例函数![]() 的图像交AB于点D,交BC于点E,已知A(
的图像交AB于点D,交BC于点E,已知A(![]() ,0),∠DOE=30°,则k的值为( )
,0),∠DOE=30°,则k的值为( )
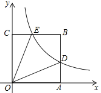
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com