
【题目】已知抛物线![]() :
:![]() (
(![]() 为常数)的顶点为
为常数)的顶点为![]() .
.
(1)求点![]() 的坐标;(用含
的坐标;(用含![]() 的式子表示)
的式子表示)
(2)在同一平面直角坐标系中,存在函数图象![]() ,点
,点![]() 在图象
在图象![]() 上,点
上,点![]() 在抛物线
在抛物线![]() 上,对于任意的实数
上,对于任意的实数![]() ,都有点
,都有点![]() ,
,![]() 关于点
关于点![]() 对称.
对称.
①当![]() 时,求图象
时,求图象![]() 对应函数的解析式;
对应函数的解析式;
②当![]() 时,都有
时,都有![]() 成立,结合图象,求
成立,结合图象,求![]() 的取值范围.
的取值范围.
【答案】(1)顶点![]() 的坐标为
的坐标为![]() ;(2)①
;(2)①![]() ,②所求
,②所求![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
【解析】
(1)把二次函数化为顶点式,即可得到答案;
(2)①根据题意,由轴对称的性质,有![]() ,然后整理得到
,然后整理得到![]() ,即可得到答案;
,即可得到答案;
②根据题意,由两个函数图形的性质,可分成3种情况进行分析,画出图像,分别求出t的取值范围即可.
(1)![]()
![]()
![]()
∴顶点![]() 的坐标为
的坐标为![]() ;
;
(2)①当![]() 时,得
时,得![]() 的解析式为:
的解析式为:![]() ,
,
点![]() 在
在![]() 上,∴
上,∴![]()
∵点![]() 与点
与点![]() 关于点
关于点![]() 对称,则点
对称,则点![]() ,
,![]() 到点
到点![]() 的距离相等,此三点横坐标相同,有
的距离相等,此三点横坐标相同,有![]() .
.
∴![]()
整理,得![]() ,
,
由于![]() 为任意实数,令
为任意实数,令![]() 为自变量
为自变量![]() ,
,![]() 为
为![]() .
.
即可得![]() 的解析式为:
的解析式为:![]() ;
;
②关于抛物线![]() 的性质:
的性质:
点![]() 在
在![]() 上,∴
上,∴![]()
由![]() :
:![]() ,知
,知
抛物线![]() 开口向上,对称轴为
开口向上,对称轴为![]() ,顶点
,顶点![]() ,且图象恒过点
,且图象恒过点![]() .
.
∴当![]() 时,图象
时,图象![]() 的
的![]() 随着
随着![]() 的增大而增大.
的增大而增大.
当![]() 时,
时,![]() 取最大值
取最大值![]() ;当
;当![]() 时,
时,![]() 取最小值
取最小值![]() ;
;
最大值比最小值大1.
关于图象![]() 的性质:
的性质:
∵点![]() 与点
与点![]() 关于点
关于点![]() 对称,
对称,
有![]() ,
,
![]() ,
,
整理,得![]()
所以,图象![]() 的解析式为:
的解析式为:![]() .
.
配方,得![]()
∴图象![]() 为一抛物线,开口向下,对称轴为
为一抛物线,开口向下,对称轴为![]() ,顶点
,顶点![]() ,且图象恒过点
,且图象恒过点![]() .
.
∴当![]() 时,图象
时,图象![]() 的
的![]() 随着
随着![]() 的增大而增大.
的增大而增大.
当![]() 时,
时,![]() 取最大值
取最大值![]() ;当
;当![]() 时,
时,![]() 取最小值
取最小值![]() ,即过
,即过![]() ;最大值比最小值大1.
;最大值比最小值大1.
情况1:当![]() ,
,![]() 两点重合,即两个函数恰好都经过
两点重合,即两个函数恰好都经过![]() ,
,![]() 时,把
时,把![]() 代入
代入![]() 得
得![]() ,解得,
,解得,![]() 或
或![]() .
.
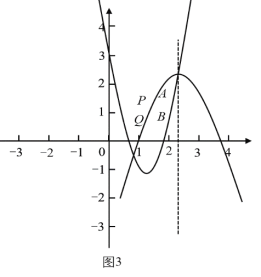
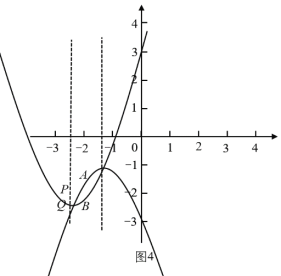
分别对应图3,图4两种情形,由图可知,当![]() ,或
,或![]() 时,
时,![]() 与
与![]() 重合,即有
重合,即有![]() ,不合题意,舍去;
,不合题意,舍去;

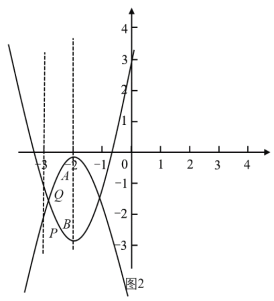
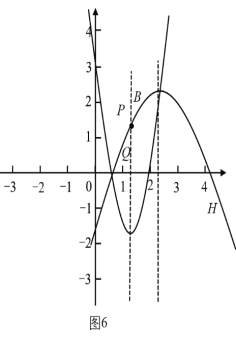
情况2:当点![]() 在点
在点![]() 下方,即
下方,即![]() 时,大致图象如图1,当
时,大致图象如图1,当![]() 时,大致图象如图2,都有点
时,大致图象如图2,都有点![]() 在点
在点![]() 的上方,即
的上方,即![]() 成立,符合题意;
成立,符合题意;
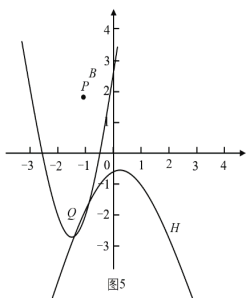
情况3:当点![]() 在点
在点![]() 上方,即
上方,即![]() 时,大致图象如图5,图6,当
时,大致图象如图5,图6,当![]() 时,存在
时,存在![]() 在
在![]() 的下方,即存在
的下方,即存在![]() ,不符合题意,舍去;
,不符合题意,舍去;
综上所述,所求![]() 的取值范围为:
的取值范围为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
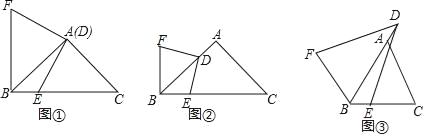
【题目】观察猜想:(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是 ,BE+BF= ;
探究证明:(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;
拓展延伸:(3)如图③,在△ABC中,AB=AC,∠BAC=a,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=a,连接BF,则BE+BF的值是多少?请用含有n,a的式子直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,新型冠状病毒席卷全球,疫情当前,全国上下砥砺同行.某中学校指导中心为引导未成年人以健康心理、阳光心态抗击疫情,积极开展了心理援助工作,并推出“你是我的奥特曼”有奖征稿活动.活动结束后,该指导中心对参赛学生的获奖情况进行统计,并绘制了如下两幅不完整的统计图.
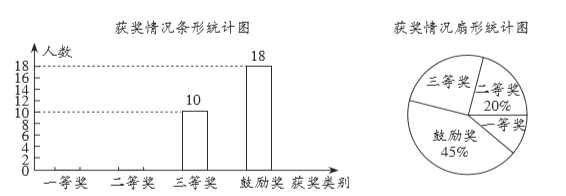
结合图中的相关数据,解答下列问题:
(1)参加此次有奖征稿活动的学生有 人,在扇形统计图中,“三等奖”所对应扇形的圆心角度数为 ;
(2)将条形统计图补充完整;
(3)若获得“一等奖”的学生中有![]() 来自七年级,
来自七年级,![]() 来自九年级,其余来自八年级,学校决定从获得“一等奖”的学生中任选2名作为代表在线上分享心灵战“疫”小锦囊,请用列表或画树状图的方法求所选2名学生中恰好是1名七年级和1名九年级学生的概率.
来自九年级,其余来自八年级,学校决定从获得“一等奖”的学生中任选2名作为代表在线上分享心灵战“疫”小锦囊,请用列表或画树状图的方法求所选2名学生中恰好是1名七年级和1名九年级学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情发生后,为支援疫情防控,某企业研发14条口罩生产线,生产普通防护口罩和普通N95口罩,现日总产量达170万只.已知每条生产线可日产普通防护口罩15万只或普通N95口罩5万只.
(1)将170万用科学记数法表示为 ;
(2)这14条生产线中,生产普通防护口罩和普通N95口罩的生产线分别有多少条?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=x-1交x轴、y轴于A、B点,点P(1,![]() ,且S四边形PAOB=3.5,双曲线y=
,且S四边形PAOB=3.5,双曲线y=![]() 经过点P.
经过点P.
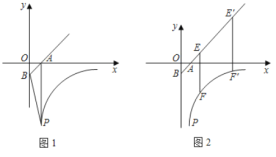
(1)求k的值;
(2)如图2,直线![]() )交射线BA于E,交双曲线y=
)交射线BA于E,交双曲线y=![]() 于F,将直线
于F,将直线![]() 向右平移4个单位长度后交射线于
向右平移4个单位长度后交射线于![]() ,交双曲线y=
,交双曲线y=![]() 于
于![]() ,若
,若![]()
![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
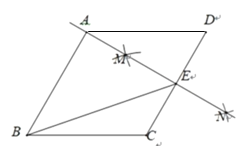
【题目】如图,在菱形ABCD中,按以下步骤作图:
①分别以点C和点D为圆心,大于![]() 的同样的长为半径作弧,两弧交于M,N两点;
的同样的长为半径作弧,两弧交于M,N两点;
②作直线MN,交CD于点E,连接BE.
若直线MN恰好经过点A,则下列说法错误的是( )
A.ABC60°
B.![]()
C.若AB4,则BE![]()
D.tanCBE![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售![]() 型和
型和![]() 型两种学习机,其中用10000元采购
型两种学习机,其中用10000元采购![]() 型学习机台数和用8000元采购
型学习机台数和用8000元采购![]() 型学习机台数相等,且一台
型学习机台数相等,且一台![]() 型学习机比一台
型学习机比一台![]() 型学习机进价多100元.
型学习机进价多100元.
(1)求一台![]() 型和
型和![]() 型学习机价格各是多少元?
型学习机价格各是多少元?
(2)若购进![]() 型学习机共100台,其中
型学习机共100台,其中![]() 型的进货量不超过
型的进货量不超过![]() 型的2倍,设购进
型的2倍,设购进![]() 型学习机
型学习机![]() 台.
台.
①求![]() 的取值范围.
的取值范围.
②已知![]() 型学习机售价均是900元/台,实际进货时,厂家对
型学习机售价均是900元/台,实际进货时,厂家对![]() 型学习机在原进货价的基础,上下调
型学习机在原进货价的基础,上下调![]() 元,且限定商店最多购进
元,且限定商店最多购进![]() 型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润
型学习机60台,若商店保持同种学习机的售价不变,请你根据以上信息,求出使这100台学习机销售总利润![]() (元)的最大值.
(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
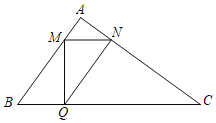
【题目】如图,在ABC中,∠A=90°,AB=3,AC=4,点M、Q分别是边AB、BC上的动点(点M不与A、B重合),且MQ⊥BC,过点M作MN∥BC.交AC于点N,连接NQ,设BQ=x.
(1)是否存在一点Q,使得四边形BMNQ为平行四边形,并说明理由;
(2)当BM=2时,求x的值;
(3)当x为何值时,四边形BMNQ的面积最大,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com