
【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.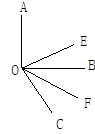
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
【答案】
(1)解:∵∠AOC=∠AOB+∠BOC,
∴∠AOC=90°+60°=150°.
∵OE平分∠AOC,
∴∠EOC=150°÷2=75°.
∵OF平分∠BOC,
∴∠COF=60°÷2=30°.
∵∠EOC=∠EOF+∠COF,
∴∠EOF=75°-30°=45°
(2)解:∵OE平分∠AOC,OF平分∠BOC.
∴∠COE= ![]() ∠AOC,∠COF=
∠AOC,∠COF= ![]() ∠BOC
∠BOC
∵∠AOB=∠AOC-∠BOC
∴∠EOF=∠COE-∠COF= ![]() ∠AOC-
∠AOC- ![]() ∠BOC=
∠BOC= ![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)= ![]() ∠AOB
∠AOB
(3)解:∵OE平分∠AOC,OF平分∠BOC,
∴∠COE= ![]() ∠AOC,∠COF=
∠AOC,∠COF= ![]() ∠BOC,
∠BOC,
∴∠EOF= ![]() ∠AOC-
∠AOC- ![]() ∠BOC=
∠BOC= ![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)= ![]() ∠AOB.又∵∠AOB+∠EOF=156°,
∠AOB.又∵∠AOB+∠EOF=156°,
∴∠EOF=52°
【解析】(1)首先求出∠AOC的度数,再根据角平分线的性质计算出∠EOC,∠BOF的度数,然后根据角的和差关系即可算出∠EOF的度数;
(2)根据角平分线的定义得出∠COE= ![]() ∠AOC,∠COF=
∠AOC,∠COF= ![]() ∠BOC ,又因∠AOB=∠AOC-∠BOC ,从而得出∠EOF=∠COE-∠COF=
∠BOC ,又因∠AOB=∠AOC-∠BOC ,从而得出∠EOF=∠COE-∠COF= ![]() ∠AOC-
∠AOC- ![]() ∠BOC=
∠BOC= ![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)= ![]() ∠AOB ;
∠AOB ;
(3)根据角平分线的定义得出∠COE= ![]() ∠AOC,∠COF=
∠AOC,∠COF= ![]() ∠BOC ,根据角的和差得出∠EOF=
∠BOC ,根据角的和差得出∠EOF= ![]() ∠AOC-
∠AOC- ![]() ∠BOC=
∠BOC= ![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)= ![]() ∠AOB.又∠AOB+∠EOF=156°,从而得出∠EOF=52° 。
∠AOB.又∠AOB+∠EOF=156°,从而得出∠EOF=52° 。


科目:初中数学 来源: 题型:
【题目】给出一种运算:对于函数y=xn,规定y′=nxn﹣1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
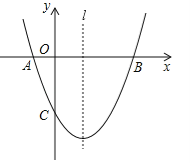
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4.
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
A. 1个或2个或3个 B. 0个或1个或2个或3个
C. 1个或2个 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( ) 
A.50°
B.51°
C.51.5°
D.52.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABD和等边三角形CBD的边长均为a,现把它们拼合起来,E是AD上异于A、D两点的一动点,F是CD上一动点,满足AE+CF=a.则△BEF的形状如何?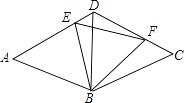
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com