
 如图所示,已知一长为2$\sqrt{3}$dm,宽为2dm的长方形木块在桌面上做无滑动的翻滚,点A翻滚第一次到达点A1,翻滚到第二次时到达点A2,则点A经过的路线与x轴和y轴围成图形的面积为(4$\sqrt{3}$+5π)dm2.
如图所示,已知一长为2$\sqrt{3}$dm,宽为2dm的长方形木块在桌面上做无滑动的翻滚,点A翻滚第一次到达点A1,翻滚到第二次时到达点A2,则点A经过的路线与x轴和y轴围成图形的面积为(4$\sqrt{3}$+5π)dm2. 分析 根据勾股定理求得AB的长,依据点A经过的路线与x轴和y轴围成图形的面积为S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$列式计算可得.
解答 解:∵AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4,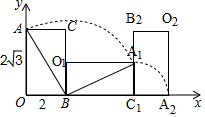
∴点A经过的路线与x轴和y轴围成图形的面积为S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$
=$\frac{1}{2}$×2$\sqrt{3}$×2+$\frac{90•π•{4}^{2}}{360}$+$\frac{90•π•{2}^{2}}{360}$+$\frac{1}{2}$×2$\sqrt{3}$×2
=4$\sqrt{3}$+5π,
故答案为:(4$\sqrt{3}$+5π)dm2.
点评 本题主要考查轨迹和勾股定理、扇形的面积,根据题意画出图形得出点A经过的路线与x轴和y轴围成图形的面积为S△AOB+${S}_{扇形AB{A}_{1}}$+${S}_{扇形{A}_{1}{C}_{1}{A}_{2}}$+${S}_{△{A}_{1}B{C}_{1}}$是解题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:解答题
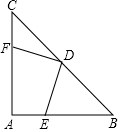 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3+5}$=$\sqrt{3}$+$\sqrt{5}$ | B. | $\sqrt{3×5}$=$\sqrt{3}$×$\sqrt{5}$ | C. | $\frac{\sqrt{24}}{\sqrt{6}}$=$\sqrt{\frac{24}{6}}$ | D. | ($\sqrt{2}$)3=2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
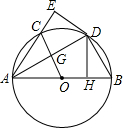 如图,AB为⊙O的直径,点D在⊙O上,DH⊥AB于H,现将△AHD沿AD翻折得到△AED,AE交⊙O于点C,连接OC交AD于点G.
如图,AB为⊙O的直径,点D在⊙O上,DH⊥AB于H,现将△AHD沿AD翻折得到△AED,AE交⊙O于点C,连接OC交AD于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com