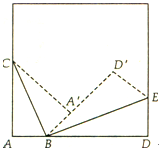
(1)由于△A′CB与△ACB关于BC对称,即△A′CB≌△ACB,那么∠A′BC=∠ABC,同理∠D′BE=∠DBE,
而∠A′BC+∠ABC+∠D′BE+∠DBE=180°,从而易求∠A′BC+∠D′BE=90°,即可证BC⊥BE;
(2)由(1)知△A′CB≌△ACB,那么∠BA′C=∠A=90°,即∠A′CB+∠CBA′=90°,而∠A′BC+∠D′BE=90°,利用等角的余角相等可知∠CBA′=∠D′BE,即知∠ACB=∠A′CB=∠D′BE=∠DBE,也就易求∠D′BE的余角、补角;
(3)由∠EBD=33°,知∠D′BD=66°,利用对顶角相等可知∠ABF=66°,从而易求∠A′BA,也就可求∠CBA.
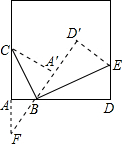
解:(1)BC⊥BE;
∵△A′CB与△ACB关于BC对称,
∴△A′CB≌△ACB,
∴∠A′BC=∠ABC,
同理有∠D′BE=∠DBE,
又∵∠A′BC+∠ABC+∠D′BE+∠DBE=180°,
∴∠A′BC+∠D′BE=90°,
∴BC⊥BE;
(2)由(1)知△A′CB≌△ACB,
∴∠BA′C=∠A=90°,
∴∠A′CB+∠CBA′=90°,
又∵∠A′BC+∠D′BE=90°,
∴∠CBA′=∠D′BE,
同理∠ACB=∠A′CB=∠D′BE=∠DBE,
∴∠D′BE的余角是∠CBA′,∠CBA,∠BED,∠BED′,补角是∠ABE;
(3)∵∠EBD=33°,
∴∠D′BD=66°,
∴∠ABF=66°,
∴∠A′BA=180°-66°=114°,
∴∠CBA=1/2×114°=57°




 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 APB绕点B按逆时针方向旋转90°
APB绕点B按逆时针方向旋转90°
 中,
中, ,
, ,
, .
.
 、
、 表示
表示 、
、 ;(直接写出答案)
;(直接写出答案) 分别在
分别在 、
、 方向上的分向量.
方向上的分向量. ,若设小路
,若设小路