
| A.对角线互相平分 | B.对角线相等 | C.对角线互相垂直 | D.两组对角分别相等 |
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:不详 题型:填空题
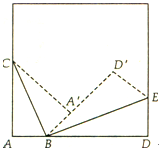
 ,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下列结论:
,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下列结论: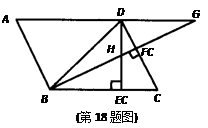
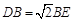 ;②
;②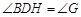 ;③AB = BH;④
;③AB = BH;④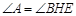 ;⑤BH = HG.
;⑤BH = HG.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 止.设运动时间为t秒.已知当t=
止.设运动时间为t秒.已知当t= 时,四边形APQD是平行四边形.
时,四边形APQD是平行四边形.
 )线段PQ是否可能平分对角线BD?若能,求t的值,若不能,请说
)线段PQ是否可能平分对角线BD?若能,求t的值,若不能,请说 明理由;
明理由;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
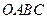 的顶点
的顶点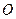 在原点,点
在原点,点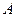 在
在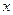 轴的正半轴上,点
轴的正半轴上,点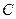 在
在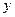 轴的正半轴上.已知
轴的正半轴上.已知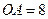 ,
,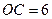 ,
,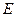 是
是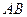 的中点,
的中点,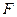 是
是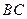 的中点.
的中点.
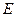 、点
、点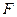 的坐标;
的坐标;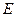 作
作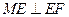 交
交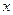 轴于点
轴于点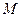 ,求点
,求点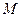 的坐标;
的坐标;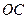 上是否存在点
上是否存在点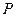 ,使得以点
,使得以点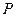 、
、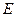 、
、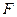 为顶点的三角形是等腰三角形,若存在,求出点
为顶点的三角形是等腰三角形,若存在,求出点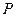 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com