
【题目】在对边不相等的四边形中,若四边形的两条对角线互相垂直,那么顺次连结四边形各边中点得到的四边形是( )
A.梯形B.矩形C.菱形D.正方形
【答案】B
【解析】
根据三角形中位线的性质,可得到这个四边形是平行四边形,再由对角线垂直,能证出有一个角等于90°,则这个四边形为矩形.
解:如图,
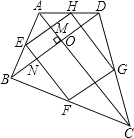
AC⊥BD,E、F、G、H分别为各边的中点,连接EF、FG、GH、HE.
∵E、F、G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD(三角形的中位线平行于第三边),
∴四边形EFGH是平行四边形(两组对边分别平行的四边形是平行四边形),
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形(有三个角是直角的四边形是矩形),
∴∠MEN=90°,
∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).
故选:B.


科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c的图像与x 轴交于A、B两点,与y轴交于点C,OB=OC.点D在函数图像上,CD//x轴,且CD=2,直线l 是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c 的值;
(2)如图①,连接BE,线段OC 上的点F 关于直线l 的对称点F′ 恰好在线段BE上,求点F的坐标;
(3)如图②,动点P在线段OB上,过点P 作x 轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.

图 ① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC

(1)线段BC的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线BA交于点D,使线段OD的长等于![]() ;
;
②连OD,在OD上画出点P,使OP得长等于![]() ,请写出画法,并说明理由.
,请写出画法,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,多项式的因式分解就是将一个多项式化成几个整式的积的形式.通过因式分解,我们常常将一个次数比较高的多项式转化成几个次数较低的整式的积,来达到降次化简的目的.这个思想可以引领我们解决很多相对复杂的代数问题.
例如:方程![]() 就可以这样来解:
就可以这样来解:
解:原方程可化为:![]()
所以![]() 或者
或者![]()
解方程![]() 得:
得:![]()
所以原方程的解:![]() ,
,![]()
根据你的理解,结合所学知识,解决以下问题:
(1)解方程:![]() ;
;
(2)已知![]() 的三边为4、x、y,请你判断代数式
的三边为4、x、y,请你判断代数式![]() 的值的符号.
的值的符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
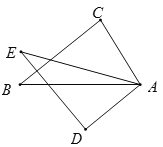
【题目】如图,已知,![]() ,AC=AD.给出下列条件: ①AB=AE;②BC=ED;③
,AC=AD.给出下列条件: ①AB=AE;②BC=ED;③![]() ;④
;④ ![]() .其中能使
.其中能使![]() 的条件为__________ (注:把你认为正确的答案序号都填上).
的条件为__________ (注:把你认为正确的答案序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个函数的解析式等于另两个函数解析式的和,则这个函数称为另两个函数的“生成函数”。现有关于x的两个二次函数y1、y2,且y1=a(x-m)2+4(m>0),y1、y2的“生成函数”为:y=x2+4x+14;当x=m时,y2=15;二次函数y2的图象的顶点坐标为(2,k)。
(1)求m的值;
(2)求二次函数y1、y2的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加一个条件使△ABC≌△DCB,下列添加的条件不能使△ABC≌△DCB的是( )

A. ∠A=∠D B. AB=DC C. AC=DB D. OB=OC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com