
【题目】我们知道,多项式的因式分解就是将一个多项式化成几个整式的积的形式.通过因式分解,我们常常将一个次数比较高的多项式转化成几个次数较低的整式的积,来达到降次化简的目的.这个思想可以引领我们解决很多相对复杂的代数问题.
例如:方程![]() 就可以这样来解:
就可以这样来解:
解:原方程可化为:![]()
所以![]() 或者
或者![]()
解方程![]() 得:
得:![]()
所以原方程的解:![]() ,
,![]()
根据你的理解,结合所学知识,解决以下问题:
(1)解方程:![]() ;
;
(2)已知![]() 的三边为4、x、y,请你判断代数式
的三边为4、x、y,请你判断代数式![]() 的值的符号.
的值的符号.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△在ABC中,∠C=90°,∠B=30°,以A为圆心、任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,给出下列说法:①DM=DN;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3,其中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,给出下列说法:①DM=DN;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3,其中正确的个数是( )
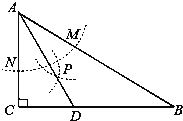
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(m+n+1)x+m(n≥0)的两个实数根为α、β,且α≤β.
(1)试用含α、β的代数式表示m和n;
(2)求证:α≤1≤β;
(3)若点P(α,β)在△ABC的三条边上运动,且△ABC顶点的坐标分别为A(1,2)、B(![]() ,1)、C(1,1),问是否存在点P,使m+n=
,1)、C(1,1),问是否存在点P,使m+n=![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.

②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是![]() 年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
甲厂:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙厂:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙厂:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
请回答下列问题:
![]() 分别求出以上三组数据的平均数、众数、中位数;
分别求出以上三组数据的平均数、众数、中位数;
![]() 这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数;
这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数;
![]() 如果你是顾客,宜选购哪家工厂的产品?为什么?
如果你是顾客,宜选购哪家工厂的产品?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
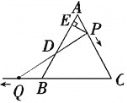
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)若AE=1时,求AP的长;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 点的纵坐标为
点的纵坐标为![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 若点
若点![]() 是反比例函数
是反比例函数![]() 图象上的一点,且满足
图象上的一点,且满足![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,请直接写出点
倍,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 和
和![]() 中,
中,![]() 为
为![]() 边
边![]() 上一点,
上一点,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.

(1)求证:![]()
(2)如图(2),若![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,![]() 为边
为边![]() 上一点,满足
上一点,满足![]() ,连接
,连接![]() 交
交![]() 于
于![]() . ①求
. ①求![]() 的度数;
的度数;
②若![]() 平分
平分![]() ,试说明:
,试说明:![]() 平分
平分![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com