
【题目】若一个函数的解析式等于另两个函数解析式的和,则这个函数称为另两个函数的“生成函数”。现有关于x的两个二次函数y1、y2,且y1=a(x-m)2+4(m>0),y1、y2的“生成函数”为:y=x2+4x+14;当x=m时,y2=15;二次函数y2的图象的顶点坐标为(2,k)。
(1)求m的值;
(2)求二次函数y1、y2的解析式。
【答案】(1)m=1;(2) y1=4x2-8x+8,y2=-3x2+12x+6.
【解析】
(1)根据已知新定义和当x= m时,y2= 15得出15= m2- a(m- m)2+4m + 10,求出即可;
(2)把m的值代入函数y2,根据顶点的横坐标即可求出a,再把a的值代入求出即可.
解:(1)由“生成函数”的概念,可知y=y1+y2.
∵y1=a(x-m)2+4,y=x2+4x+14,
∴y2=y-y1=x2+4x+14-a(x-m)2-4.
∵当x=m时,y2=15,∴15=m2+4m+10,得m1=-5,m2=1
又∵m>0,
∴m=1.
(2)由m=1得,y2=x2+4x+14-a(x-1)2-4
=(1-a)x2+(4+2a)x+10-a.
∵二次函数y2的图象的顶点坐标为(2,k),
∴对称轴x=-![]() =2,解得a=4.
=2,解得a=4.
∴y1=4(x-1)2+4=4x2-8x+8,
∴y2=(1-4)x2+(4+2×4)x+10-4=-3x2+12x+6.


科目:初中数学 来源: 题型:
【题目】如图,A、B两点的坐标分别为(0,6),(0,3),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.

(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(2,0)运动到点(3,0)时,请直接写出线段QM扫过图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.

②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
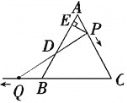
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)若AE=1时,求AP的长;
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.

(1)问题:方程x3+x2﹣2x=0的解是x1=0,x2=________,x3=________;
(2)拓展:用“转化”思想求方程![]() =x的解;
=x的解;
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 点的纵坐标为
点的纵坐标为![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 若点
若点![]() 是反比例函数
是反比例函数![]() 图象上的一点,且满足
图象上的一点,且满足![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,请直接写出点
倍,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )

A. 71° B. 76° C. 78° D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有![]() 个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共
个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共![]() 组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做
组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做![]() 次试验,汇总起来后,摸到红球次数为
次试验,汇总起来后,摸到红球次数为![]() 次.
次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com