Question

4．如图1，在四边形ABCD中，∠BAD=∠ABC=90°，点E从点C出发，以每秒1个单位长度的速度沿射线CB运动，在射线CD上取点F，且CF=CE，连接EF，当EF经过点A时，点E停止运动，△CEF与四边形ABCD重叠部分的面积为S，点E的运动时间为t秒，且知当0＜t≤2时，S=$\frac{\sqrt{3}}{4}$t²，S关于t的函数图象如图2所示，（其中0＜t≤2，2＜t≤m，m＜t≤4时，函数的解析式不同）．
（1）∠BAC=60°；
（2）求m的值；
（3）当2＜t≤4时，求S与t之间的函数关系式．

Answer 1

分析 （1）由题意知当点E运动到E时CD=CE=2，当点E运动到M时CM=CN=4，作DP⊥EC于点P，根据当t=2时，S=$\sqrt{3}$=$\frac{1}{2}$EC•DP，即$\frac{1}{2}$×2×DP=$\sqrt{3}$得DP=AB=$\sqrt{3}$，从而知∠C=60°，进而得△CMN是等边三角形且MN=CN=MC=4、CP=$\frac{1}{2}$CE=1，由AD∥BC知△ADN是等边三角形，得出AN=AM=2，结合等腰三角形性质知∠CAM=90°、Rt△ABM中根据cos$∠BAM=\frac{AB}{AM}$=$\frac{\sqrt{3}}{2}$可得∠BAM=30°，依据∠CAB=∠CAM-∠BAM得出答案；
（2）当点E运动到点B位置时CB=m，在Rt△ABM中，由AM=2、∠BAM=30°知BM=$\frac{1}{2}$AM=1，从而得CB=CM-BM=4-1=3；
（3）当2＜t≤3时，由（1）知△CEF是边长为t的等边三角形、△DFG等边三角形，DF=CF-CD=t-2，根据S=S_△CEF-S_△DGF可得；当3＜t≤4时，Rt△BEM中BM=BEtan∠BEM=$\sqrt{3}$（t-3），依据S=S_△CEF-S_△DNF-S_△BEM可得．

解答 解：（1）如图1，由题意知当点E运动到E时，CD=CE=2，当点E运动到M时，CM=CN=4，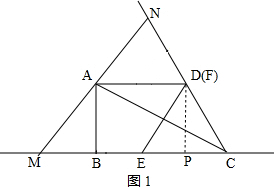

作DP⊥EC于点P，
当t=2时，S=$\frac{\sqrt{3}}{4}$t²=$\sqrt{3}$=$\frac{1}{2}$EC•DP，即$\frac{1}{2}$×2×DP=$\sqrt{3}$，
∴DP=AB=$\sqrt{3}$，
在Rt△CDP中，∵sinC=$\frac{DP}{DC}$=$\frac{\sqrt{3}}{2}$，
∴∠C=60°，
∴△CMN是等边三角形，且MN=CN=MC=4，
∴CP=$\frac{1}{2}$CE=1，
∵四边形ABCD中，∠BAD=∠ABC=90°，
∴AD∥BC，
∴∠ADN=60°，
∴△ADN是等边三角形，且AD=AN=DN=CN-CD=4-2=2，
∴AM=MN-AN=2=AN，
∴CA⊥MN，即∠CAM=90°，
在Rt△ABM中，∵AM=2，AB=$\sqrt{3}$，
∴cos$∠BAM=\frac{AB}{AM}$=$\frac{\sqrt{3}}{2}$，
∴∠BAM=30°，
∴∠CAB=∠CAM-∠BAM=60°，
故答案为：60°；

（2）当点E运动到点B位置时，CB=m，
在Rt△ABM中，∵AM=2，∠BAM=30°，
∴BM=$\frac{1}{2}$AM=1，
∴CB=CM-BM=4-1=3，
即m=3；

（3）如图2，当2＜t≤3时，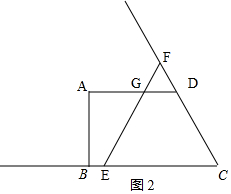

由（1）知，∠C=60°，且CE=CF=t，CD=2，
∴△CEF是边长为t的等边三角形，
∴∠CFE=60°，
∵AD∥BC，
∴∠FDG=∠C=60°，
∴△DFG等边三角形，DF=CF-CD=t-2，
则S=S_△CEF-S_△DGF=$\frac{\sqrt{3}}{4}$t²-$\frac{\sqrt{3}}{4}$（t-2）²=$\sqrt{3}$t-$\sqrt{3}$；
当3＜t≤4时，如图3，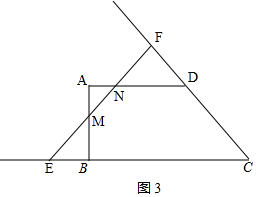

∵△CEF和△DNF是等边三角形，CE=CF=t，CD=2，BC=3
∴DF=CF-CD=t-2，BE=CE-BC=t-3，
在Rt△BEM中，BM=BEtan∠BEM=$\sqrt{3}$（t-3），
则S=S_△CEF-S_△DNF-S_△BEM=$\frac{\sqrt{3}}{4}$t²-$\frac{\sqrt{3}}{4}$（t-2）²-$\frac{1}{2}$×（t-3）•$\sqrt{3}$（t-3）=-$\frac{\sqrt{3}}{2}$t²+4$\sqrt{3}$t-$\frac{11\sqrt{3}}{2}$，
综上，S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{4}{t}^{2}}&{（0＜t≤2）}\\{\sqrt{3}t-\sqrt{3}}&{（2＜t≤3）}\\{-\frac{\sqrt{3}}{2}{t}^{2}+4\sqrt{3}t-\frac{11\sqrt{3}}{2}}&{（3＜t≤4）}\end{array}\right.$．

点评 本题主要考查四边形的综合，涉及的知识点有等边三角形的判定与性质、矩形的判定与性质、解直角三角形及等边三角形的面积，根据函数图象得出t=2和t=4时的临界情况在变化过程中的所表示的线段长是关键．