
【题目】如图,点A,B在反比例函数y= ![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 . 
【答案】![]()
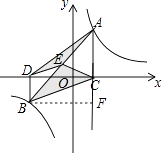
【解析】解:过点B作直线AC的垂线交直线AC于点F,如图所示. ∵△BCE的面积是△ADE的面积的2倍,E是AB的中点,
∴S△ABC=2S△BCE , S△ABD=2S△ADE ,
∴S△ABC=2S△ABD , 且△ABC和△ABD的高均为BF,
∴AC=2BD,
∴OD=2OC.
∵CD=k,
∴点A的坐标为( ![]() ,3),点B的坐标为(﹣
,3),点B的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴AC=3,BD= ![]() ,
,
∴AB=2AC=6,AF=AC+BD= ![]() ,
,
∴CD=k= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用比例系数k的几何意义对题目进行判断即可得到答案,需要熟知几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.


科目:初中数学 来源: 题型:
【题目】湖州某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 15 | 12 |
月污水处理能力(吨/月) | 250 | 200 |
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y= ![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 . 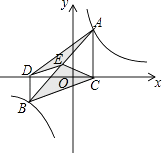
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )

A. BC=EC,∠B=∠E B. BC=DC,∠A=∠D
C. BC=EC,AC=DC D. AC=DC,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO. 
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式.
(2)若α为锐角,tanα= ![]() ,当AE取得最小值时,求正方形OEFG的面积.
,当AE取得最小值时,求正方形OEFG的面积.
(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为 ![]() :1?若能,求点P的坐标;若不能,试说明理由
:1?若能,求点P的坐标;若不能,试说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com