
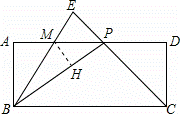
已知在矩形ABCD中,P是边AD上的一动点,联结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y;
(1)求y关于x的函数解析式,并写出 它的定义域;
它的定义域;
(2)当AP=4时,求∠EBP的正切值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长.
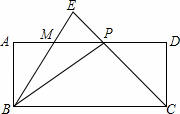
解:(1)∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=5,∠A=∠D=90°,AD∥BC,
∴∠APB=∠PBC.
∵∠ABE=∠CBP,
∴∠ABM=∠APB.
又∵∠A=∠A,
∴△ABM∽△APB,
∴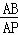 =
=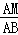 ,
,
∴ =
=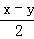 ,
,
∴y=x﹣ .
.
∵P是边AD上的一动点,
∴0≤x≤5.
∵y>0,
∴x﹣ >0,
>0,
∴x>2,
∴函数的定义域为2<x≤5;
(2)过点M作MH⊥BP于H,如图.
∵AP=x=4,∴y=x﹣ =3,
=3,
∴MP=3,AM=1,
∴BM=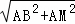 =
=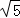 ,BP=
,BP=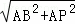 =2
=2 .
.
∵S△BMP=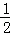 MP•AB=
MP•AB=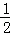 BP•MH,
BP•MH,
∴MH=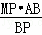 =
=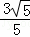 ,
,
∴BH= =
= ,
,
∴tan∠EBP= =
=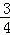 ;
;
(3)①若EB=EC,
则有∠EBC=∠ECB.
∵AD∥BC,
∴∠AMB=∠EBC,∠DPC=∠ECB,
∴∠AMB=∠DPC.
在△AMB和△DPC中,
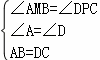 ,
,
∴△AMB≌△DPC,
∴AM=DP,
∴x﹣y=5﹣x,
∴y=2x﹣5,
∴x﹣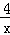 =2x﹣5,
=2x﹣5,
解得:x1=1,x2=4.
∵2<x≤5,
∴AP=x=4;
②若CE=CB,
则∠EBC=∠E.
∵AD∥BC,
∴∠EMP=∠EBC=∠E,
∴PE=PM=y,
∴PC=EC﹣EP=5﹣y,
∴在Rt△DPC中,
(5﹣y)2﹣(5﹣x)2=22,
∴(10﹣x﹣y)(x﹣y)=4,
∴(10﹣x﹣x+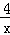 )(x﹣x+
)(x﹣x+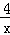 )=4,
)=4,
整理得:3x2﹣10x﹣4=0,
解得:x3=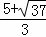 ,x4=
,x4=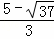 (舍负).
(舍负).
∴AP=x=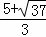 .
.
终上所述:AP的值为4或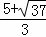 .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5 月份A款汽车每辆售价多少万元?
月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )

A. 1 B.2 C.3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
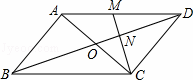
如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线点F.问:
(1)图中△APD与哪个三角形全等?并说明理由;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE ,PF之间存在什么关系?并说明理由.
,PF之间存在什么关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com