
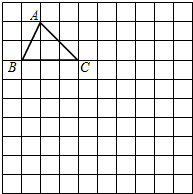
 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.分析 (1)由平移的性质容易得到△A′B′C′;
(2)由平移的性质和旋转的性质容易画出图形;
(3)由弧长公式求出$\widehat{B′B″}$的长,点B经过(1),(2)两次变换的路径长=BB′+$\widehat{B′B″}$的长,即可得出结果.
解答 解:(1)将△ABC向下平移4个单位,得到△A′B′C′,如图1所示: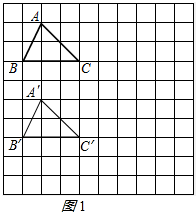
(2)把△A′B′C′绕点C′顺时针旋转90°,得到△A″B″C″,
如图2所示: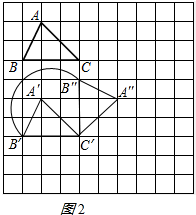
(3)根据题意得:BB′=4,B′C′=3,
$\widehat{B′B″}$的长=$\frac{90π×3}{180}$=$\frac{3π}{2}$,
故点B经过(1),(2)两次变换的路径长=BB′+$\widehat{B′B″}$的长=4+$\frac{3π}{2}$.
点评 本题考查了作图-平移变换、作图-旋转变换、弧长公式;熟练掌握平移和旋转的性质,并能进行作图与计算是解决问题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:填空题
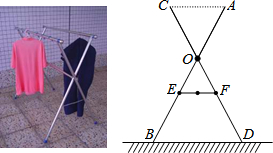
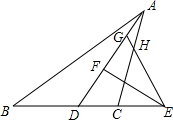 如图,在△ABC中,2AB=3AC,AD为△BAC的角平分线,点H在线段AC上,且CH=2AH,E为BC延长线上的一点,连接EH并延长交AD于点G,使EG=ED,过点E作EF⊥AD于点F,则AG:FG=4:7.
如图,在△ABC中,2AB=3AC,AD为△BAC的角平分线,点H在线段AC上,且CH=2AH,E为BC延长线上的一点,连接EH并延长交AD于点G,使EG=ED,过点E作EF⊥AD于点F,则AG:FG=4:7.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 120元 | B. | 130元 | C. | 140元 | D. | 150元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
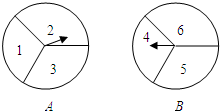 如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,
如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com