
分析 先根据等角对等边得出∠OAC=∠OCA=$\frac{1}{2}$(180°-∠BOD)和∠OBD=∠ODB=$\frac{1}{2}$(180°-∠BOD),进而利用平行线的判定得出即可,再证明Rt△OEM∽Rt△ABH,进而得出AH的长即可.
解答 解:∵AB、CD相交于点O,
∴∠AOC=∠BOD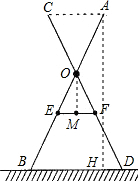
∵OA=OC,
∴∠OAC=∠OCA=$\frac{1}{2}$(180°-∠BOD),
同理可证:∠OBD=∠ODB=$\frac{1}{2}$(180°-∠BOD),
∴∠OAC=∠OBD,
∴AC∥BD,
在Rt△OEM中,OM=$\sqrt{O{E}^{2}-E{M}^{2}}$=30(cm),
过点A作AH⊥BD于点H,
同理可证:EF∥BD,
∴∠ABH=∠OEM,则Rt△OEM∽Rt△ABH,
∴$\frac{OE}{AB}$=$\frac{OM}{AH}$,AH=$\frac{OM•AB}{OE}$=$\frac{30×136}{34}$=120(cm),
所以垂挂在衣架上的连衣裙总长度小于120cm时,连衣裙才不会拖落到地面上.
故答案为:120.
点评 此题主要考查了相似三角形的判定与性质以及解直角三角形,根据已知构造直角三角形利用锐角三角函数解题是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 普查 | B. | 抽样调查 | ||
| C. | 在社会上随机调查 | D. | 在学校里随机调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
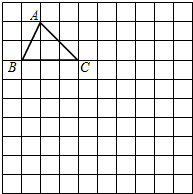 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
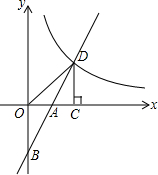 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A.B两点,与双曲线y=$\frac{k}{x}$(x>0)交于点D,过点D作DC⊥x轴,垂足为C,且点A是OC的中点,连接OD,
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A.B两点,与双曲线y=$\frac{k}{x}$(x>0)交于点D,过点D作DC⊥x轴,垂足为C,且点A是OC的中点,连接OD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com