
【题目】在长方形![]() 中,
中,![]() ,现将长方形
,现将长方形![]() 向上平移
向上平移![]() ,再向左平移
,再向左平移![]() 后到长方形
后到长方形![]() 的位置(
的位置(![]() 的对应点为
的对应点为![]() ,其它类似).
,其它类似).
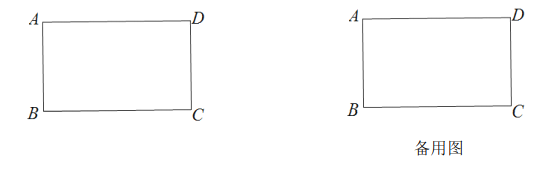
![]() 当
当![]() 时,请画出平移后的长方形
时,请画出平移后的长方形![]() ,并求出长方形
,并求出长方形![]() 与长方形
与长方形![]() 的重叠部分的面积.
的重叠部分的面积.
![]() 当
当![]() 满足什么条件时,长方形
满足什么条件时,长方形![]() 与长方形
与长方形![]() 有重叠部分(边与边叠合不算在内),请用
有重叠部分(边与边叠合不算在内),请用![]() 的代数式表示重叠部分的面积.
的代数式表示重叠部分的面积.
![]() 在平移的过程中,总会形成一个六边形
在平移的过程中,总会形成一个六边形![]() ,试用
,试用![]() 来表示六边形
来表示六边形![]() 的面积.
的面积.
【答案】(1)长方形![]() 见详解,重叠部分的面积=
见详解,重叠部分的面积=![]() ;(2)重叠部分的面积=
;(2)重叠部分的面积=![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意,画出长方形![]() ,进而可得重叠部分的面积;
,进而可得重叠部分的面积;
(2)根据题意得长方形![]() 与长方形
与长方形![]() 的重叠部分的长为
的重叠部分的长为![]() ,宽为
,宽为![]() ,从而得重叠部分的面积,由重叠部分的长与宽的实际意义,列出关于x的不等式组,进而即可求解;
,从而得重叠部分的面积,由重叠部分的长与宽的实际意义,列出关于x的不等式组,进而即可求解;
(3)延长A1D1,CD交于点M,延长A1B1,CB交于点N,根据割补法,求出六边形![]() 的面积,即可.
的面积,即可.
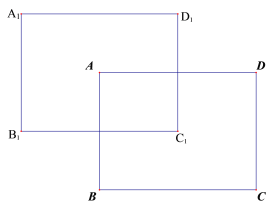
(1)长方形![]() ,如图所示:
,如图所示:
∵在长方形![]() 中,
中,![]() ,将长方形
,将长方形![]() 向上平移
向上平移![]() ,再向左平移
,再向左平移![]() 后到长方形
后到长方形![]() 的位置,
的位置,
∴长方形![]() 与长方形
与长方形![]() 的重叠部分的面积=
的重叠部分的面积=![]() ;
;
(2)∵![]() ,将长方形
,将长方形![]() 向上平移
向上平移![]() ,再向左平移
,再向左平移![]() 后到长方形
后到长方形![]() 的位置,
的位置,
∴长方形![]() 与长方形
与长方形![]() 的重叠部分的长为
的重叠部分的长为![]() ,宽为
,宽为![]() ,
,
∴重叠部分的面积=![]() ,
,
∵![]() 且
且![]() 且
且![]() ,
,
∴![]() ;
;
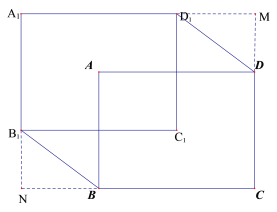
(3)延长A1D1,CD交于点M,延长A1B1,CB交于点N,
六边形![]() 的面积=
的面积=![]()
=![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】小刚同学动手剪了如图①所示![]() ,
,![]() 的正方形纸片与
的正方形纸片与![]() 的长方形纸片若干块.
的长方形纸片若干块.
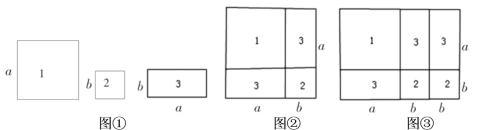
(1)小刚用1张1号、1张2号和2张3号纸片拼出一个新图形(如图②),根据这个图形的面积关系可以写出一个你所熟悉的乘法公式,这个乘法公式是 ;
(2)根据小刚用1张1号、2张2号和3张3号纸片拼成的长方形(如图③),6张纸片的面积等于所拼成大长方形的面积,将多项式![]() 因式分解,其结果是 ;
因式分解,其结果是 ;
(3)动手操作,请你依照小刚的方法,利用拼图分解因式:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:
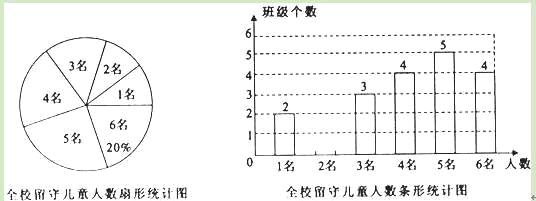
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB∥CD,点P为定点,E、F分别是AB、CD上的动点.
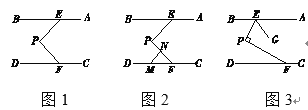
(1)求证:∠P=∠BEP+∠PFD;
(2)若点M为CD上一点,如图2,∠FMN=∠BEP,且MN交PF于N.试说明∠EPF与∠PNM的数量关系,并证明你的结论;
(3)移动E、F使得∠EPF=90°,如图3,作∠PEG=∠BEP,求∠AEG与∠PFD度数的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某铁路桥长1000米.现有一列火车从桥上匀速通过.测得火车从开始上桥到完全通过桥共用了1分钟(即从车头进入桥头到车尾离开桥尾),整个火车完全在桥上的时间为40秒.
(1)如果设这列火车的长度为x米,填写下表(不需要化简):
火车行驶过程 | 时间(秒) | 路程(米) | 速度(米/秒) |
完全通过桥 | 60 | ||
整列车在桥上 | 40 |
(2)求这列火车的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某草莓种植大户,今年从草莓上市到销售完需要20天,售价为15元/千克,成本y(元/千克)与第x天成一次函数关系,当x=10时,y=7,当x=15时,y=6.5.
(1)求成本y(元/千克)与第x天的函数关系式并写出自变量x的取值范围;
(2)求第几天每千克的利润w(元)最大?最大利润是多少?(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .
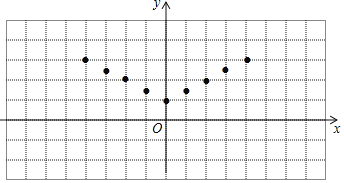
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:①已知A(x1,y1)、B(x2,y2),则AB=![]() ;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离
;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离![]()
(1)已知 A2,5、 B1,1,求 AB ;
(2)已知 A2,1,直线l : 3x 4y 5 0,求 A 到直线的距离;
(3)求两平行直线3x 4y1 0与3x 4 y 8 0之间的距离;
(4)求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com