
 ”Î
”Î ÷·Ωª”⁄µ„A(£≠1£¨0)°¢B(3£¨0)£¨”Î
÷·Ωª”⁄µ„A(£≠1£¨0)°¢B(3£¨0)£¨”Î ÷·Ωª”⁄µ„C(0£¨3)£Æ
÷·Ωª”⁄µ„C(0£¨3)£Æ
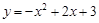 £¨£®1£¨4£©£ª(2)
£¨£®1£¨4£©£ª(2)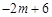 £ª (3)
£ª (3)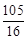 £¨£®
£¨£®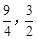 £©£ª(4) £®2£¨3£©£ª£®
£©£ª(4) £®2£¨3£©£ª£®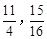 £©.
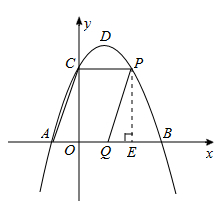
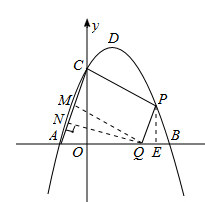
£©.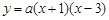 ,Ω´µ„C(0£¨3)¥˙»Îº¥ø…«Û≥ˆ≈◊ŒÔœþµƒΩ‚Œˆ Ω£¨‘ŸªØ≥…∂•µ„ Ω¥”∂¯«Û≥ˆ∂•µ„◊¯±ÍD.
,Ω´µ„C(0£¨3)¥˙»Îº¥ø…«Û≥ˆ≈◊ŒÔœþµƒΩ‚Œˆ Ω£¨‘ŸªØ≥…∂•µ„ Ω¥”∂¯«Û≥ˆ∂•µ„◊¯±ÍD.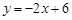 £¨°þµ„Pµƒ∫·◊¯±ÍŒ™m°ýµ„Pµƒ◊ð◊¯±ÍŒ™£∫
£¨°þµ„Pµƒ∫·◊¯±ÍŒ™m°ýµ„Pµƒ◊ð◊¯±ÍŒ™£∫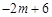 .
.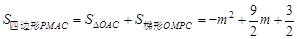 £¨‘Ÿ≈‰≥…∂•µ„ Ω
£¨‘Ÿ≈‰≥…∂•µ„ Ω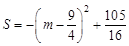 £¨°þ
£¨°þ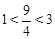 £¨°ýµ±
£¨°ýµ±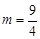 ±£¨Àƒ±þ–ŒPMACµƒ√ʪ˝»°µ√◊Ó¥Û÷µŒ™
±£¨Àƒ±þ–ŒPMACµƒ√ʪ˝»°µ√◊Ó¥Û÷µŒ™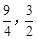 £©.
£©.
 ”Îx÷·Ωª”⁄µ„A(£≠1£¨0)°¢B(3£¨0)£¨
”Îx÷·Ωª”⁄µ„A(£≠1£¨0)°¢B(3£¨0)£¨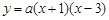
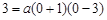
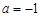
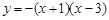
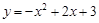
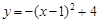
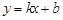
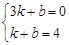
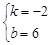
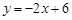
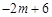
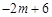
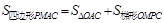
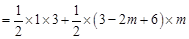
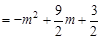
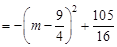
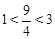 £¨°ýµ±
£¨°ýµ±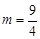 ±£¨Àƒ±þ–ŒPMACµƒ√ʪ˝»°µ√◊Ó¥Û÷µŒ™
±£¨Àƒ±þ–ŒPMACµƒ√ʪ˝»°µ√◊Ó¥Û÷µŒ™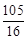 .
.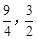 £©.
£©.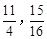 £©.
£©.

 ≥¨ƒÐ—ßµ‰”¶”√ÂÂø®œµ¡–¥∞∏
≥¨ƒÐ—ßµ‰”¶”√ÂÂø®œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫ÃÓø’Â
 …œµƒ¡Ωµ„£¨‘Úy1”Îy2µƒ¥Û–°πÿœµŒ™y1 y2£®ÃÓ°∞>°±°∞<°±ªÚ°∞£Ω°±£©£Æ
…œµƒ¡Ωµ„£¨‘Úy1”Îy2µƒ¥Û–°πÿœµŒ™y1 y2£®ÃÓ°∞>°±°∞<°±ªÚ°∞£Ω°±£©£Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
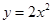 µƒÕºœÛœÚ…œ∆Ω“∆1∏ˆµ•Œª£¨‘Ú∆Ω“∆∫Ûµƒ≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™£® £©
µƒÕºœÛœÚ…œ∆Ω“∆1∏ˆµ•Œª£¨‘Ú∆Ω“∆∫Ûµƒ≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™£® £©A£Æ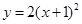 | B£Æ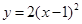 | C£Æ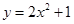 | D£Æ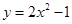 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫ÃÓø’Â
 »∆◊≈À¸”Îy÷·µƒΩªµ„–˝◊™180°„£¨À˘µ√≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™ £Æ
»∆◊≈À¸”Îy÷·µƒΩªµ„–˝◊™180°„£¨À˘µ√≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™ £Æ≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
| x | ©Å3 | ©Å2 | ©Å1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 12 | 5 | 0 | ©Å3 | ©Å4 | ©Å3 | 0 | 5 | 12 |
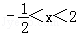 ±£¨y£º0£ª
±£¨y£º0£ª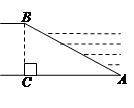
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
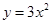 œ»œÚ…œ∆Ω“∆3∏ˆµ•Œª£¨‘ŸœÚ◊Û∆Ω“∆2∏ˆµ•Œª∫Ûµ√µΩµƒ≈◊ŒÔœþΩ‚Œˆ ΩŒ™£® £©
œ»œÚ…œ∆Ω“∆3∏ˆµ•Œª£¨‘ŸœÚ◊Û∆Ω“∆2∏ˆµ•Œª∫Ûµ√µΩµƒ≈◊ŒÔœþΩ‚Œˆ ΩŒ™£® £©A£Æ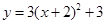 | B£Æ |
C£Æ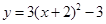 | D£Æ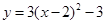 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
| x | °≠ | ©Å3 | ©Å2 | ©Å1 | 0 | 1 | °≠ |
| y | °≠ | ©Å3 | ©Å2 | ©Å3 | ©Å6 | ©Å11 | °≠ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com