
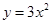 先向上平移3个单位,再向左平移2个单位后得到的抛物线解析式为( )
先向上平移3个单位,再向左平移2个单位后得到的抛物线解析式为( )A.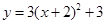 | B. |
C.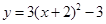 | D.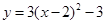 |
科目:初中数学 来源:不详 题型:解答题
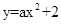 与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,
与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,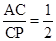 ,且S△AOC=1,过点P作PB⊥y轴于点B.
,且S△AOC=1,过点P作PB⊥y轴于点B.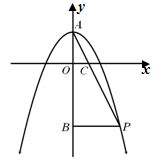
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=3x2+3 | B.y=3x2-1 | C.y=3(x-4)2+3 | D.y=3(x-4)2-1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
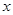 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为 元,试写出
元,试写出 与
与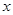 之间的函数关系式.
之间的函数关系式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与 轴交于点A(-1,0)、B(3,0),与
轴交于点A(-1,0)、B(3,0),与 轴交于点C(0,3).
轴交于点C(0,3).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.x1<x2<a<b | B.x1<a<x2<b | C.x1<a<b<x2 | D.a<x1<b<x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com