
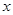 ��������㹽һ���Գ��ۣ��������㹽�������ܽ��Ϊ
��������㹽һ���Գ��ۣ��������㹽�������ܽ��Ϊ Ԫ����д��
Ԫ����д�� ��
��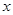 ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��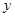 ��
�� =
=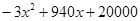 ��1��
��1��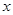 ��110����
��110����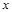 ��������
��������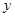 ��
�� =
=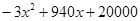 ��1��
��1��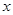 ��110����
��110����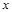 ��������
�������� ��
��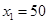 ��
��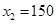 ���������⣬��ȥ��
���������⣬��ȥ�� ��
��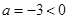 ���������߿��ڷ������£���
���������߿��ڷ������£���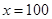 ʱ��w���=30000��
ʱ��w���=30000��

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д� �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
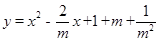 �����������y�������x֮��Ĺ�ϵʽ.
�����������y�������x֮��Ĺ�ϵʽ.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �ϵ����㣬��y1��y2�Ĵ�С��ϵΪy1 y2���>����<����������
�ϵ����㣬��y1��y2�Ĵ�С��ϵΪy1 y2���>����<�����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

| A��1 | B��2 | C��3 | D��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ,0)ΪԲ�ģ���
,0)ΪԲ�ģ��� Ϊ�뾶Բ��x���ཻ�ڵ�B��C����y���ཻ�ڵ�D��E.
Ϊ�뾶Բ��x���ཻ�ڵ�B��C����y���ཻ�ڵ�D��E.
 ������C��D���㣬�������ߵĽ���ʽ�����жϵ�B�Ƿ��ڸ��������ϣ�
������C��D���㣬�������ߵĽ���ʽ�����жϵ�B�Ƿ��ڸ��������ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��ͼ����P��-3��2�������ͼ��ؾ����㣨 ��
��ͼ����P��-3��2�������ͼ��ؾ����㣨 ��| A����2��3�� | B����-2��-3�� | C����3��2�� | D����-3��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

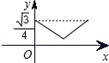 B��
B�� C��
C��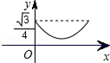 D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
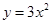 ������ƽ��3����λ��������ƽ��2����λ��õ��������߽���ʽΪ�� ��
������ƽ��3����λ��������ƽ��2����λ��õ��������߽���ʽΪ�� ��A��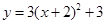 | B�� |
C��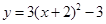 | D��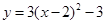 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com