
【题目】等腰三角形一腰上的高与另一腰的夹角为40°,则等腰三角形底角的度数是________________°.
【答案】65或25
【解析】
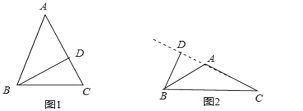
在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=40°,讨论:当BD在△ABC内部时,如图1,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形内角和可计算出∠ACB;当BD在△ABC外部时,如图2,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形外角性质可计算出∠ACB.
在等腰△ABC中,AB=AC,BD为腰AC上的高,∠ABD=40°,
当BD在△ABC内部时,如图1,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°40°=50°,
∵AB=AC,
∴∠ABC=∠ACB=![]() (180°50°)=65°;
(180°50°)=65°;
当BD在△ABC外部时,如图2,
∵BD为高,
∴∠ADB=90°,
∴∠BAD=90°40°=50°,
∵AB=AC,
∴∠ABC=∠ACB,
而∠BAD=∠ABC+∠ACB,
∴∠ACB=![]() ∠BAD=25°,
∠BAD=25°,
综上所述,这个等腰三角形底角的度数为65°或25°.
故填:65或25.


科目:初中数学 来源: 题型:
【题目】为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级、B级、C级、D级),并将那个测试结果绘成了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:

(1)本次抽样测试的学生人数是 ;
(2)扇形图中∠α的度数是 ,并把条形统计图补充完整;
(3)对A,B,C,D四个等级依次赋分为90,75,65,55(单位:分),比如:等级为A的同学体育得分为90分,…,依此类推.该市九年级共有学生32000名,如果全部参加这次体育测试,估计该市九年级不及格(即60分以下)学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A.AE=CFB.DE=BFC.∠ADE=∠CBFD.∠AED=∠CFB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,动点![]() 在第一象限及
在第一象限及![]() 、
、![]() 轴上运动.第一次它从原点
轴上运动.第一次它从原点![]() 运到点
运到点![]() ,然后按图中箭头所示方向运动,即
,然后按图中箭头所示方向运动,即![]() ,每次运动一个单位长度,若第2018次运动到点
,每次运动一个单位长度,若第2018次运动到点![]() ,则式子
,则式子![]() 的值是______.
的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和直线BC相交于点B,连接AC,点D. E. H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°,

(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.

(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;
(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG 的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习了整式的乘法,两个多项式相乘,我们可以运用法则,将其展开,例如:![]() ,而将等号的左右两边互换,我们得到了
,而将等号的左右两边互换,我们得到了![]() ,等号的左边是一个多项式,而右边是几个整式相乘的形式,我们规定将一个多项式写成几个整式相乘的形式,这种运算称之为“因式分解”
,等号的左边是一个多项式,而右边是几个整式相乘的形式,我们规定将一个多项式写成几个整式相乘的形式,这种运算称之为“因式分解”
问题提出:
如何将![]() 进行因式分解呢?
进行因式分解呢?
问题探究:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释
例如:我们可以通过表示几何图形面积的方法来快速的对多项式![]() 进行因式分解.
进行因式分解.
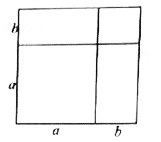
如图所示边长为![]() 的大正方形是由1个边长为
的大正方形是由1个边长为![]() 的正方形,2个边长为
的正方形,2个边长为![]() 的长方形,1个边长为
的长方形,1个边长为![]() 的正方形,
的正方形,![]() 组成,我们可以用两种方法表示大正方形的面积,这个图形的面积可以表示成:
组成,我们可以用两种方法表示大正方形的面积,这个图形的面积可以表示成:![]() 或
或![]()
∴![]()
我们将等号左边的多项式写成了右边两个整式相乘的形式,从而成功的对多项式![]() 进行了因式分解
进行了因式分解
请你类比上述方法,利用图形的几何意义对多项式![]() 进行因式分解(要求自己构图并写出推证过程)
进行因式分解(要求自己构图并写出推证过程)
问题拓展:
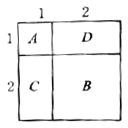
如何利用图形几何意义的方法推导:![]() ?如图,
?如图,![]() 表示1个
表示1个![]() 的正方形,即
的正方形,即![]() ,
,![]() 表示1个
表示1个![]() 的正方形,
的正方形,![]() 与
与![]() 恰好可以拼成1个
恰好可以拼成1个![]() 的正方形,因此:
的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2个
就可以表示2个![]() 的正方形,即
的正方形,即![]() ,而
,而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一个
恰好可以拼成一个![]() 的大正方形.由此可得:
的大正方形.由此可得:![]()
尝试解决:
请你类比上述推导过程,利用图形几何意义方法推导出![]() 的值.
的值.
(要求自己构造图形并写出推证过程).
解:
归纳猜想:![]() _________________.
_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
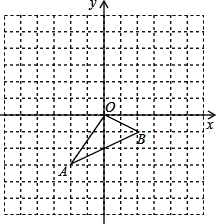
【题目】如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3).
(1)求三角形ABO的面积;
(2)作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′ 、B′ ;
(3)P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com