
【题目】已知:一组邻边分别为![]() 和
和![]() 的平行四边形
的平行四边形![]() ,
,![]() 和
和![]() 的平分线分别交
的平分线分别交![]() 所在直线于点
所在直线于点![]() ,
,![]() ,则线段
,则线段![]() 的长为________
的长为________![]() .
.
【答案】![]() 或
或![]()
【解析】
利用当AB=10cm,AD=6cm,由于平行四边形的两组对边互相平行,又AE平分∠BAD,由此可以推出所以∠BAE=∠DAE,则DE=AD=6cm;同理可得:CF=CB=6cm,而EF=CF+DE-DC,由此可以求出EF长;同理可得:当AD=10cm,AB=6cm时,可以求出EF长
解:如图1,当AB=10cm,AD=6cm
∵AE平分∠BAD
∴∠BAE=∠DAE,
又∵AD∥CB
∴∠EAB=∠DEA,
∴∠DAE=∠AED,则AD=DE=6cm
同理可得:CF=CB=6cm
∵EF=DE+CF-DC=6+6-10=2(cm)
如图2,当AD=10cm,AB=6cm,
∵AE平分∠BAD,
∴∠BAE=∠DAE
又∵AD∥CB
∴∠EAB=∠DEA,
∴∠DAE=∠AED则AD=DE=10cm
同理可得,CF=CB=10cm EF=DE+CF-DC=10+10-6=14(cm)
故答案为:2或14.
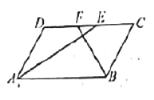
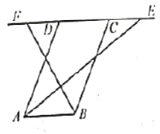
图1 图2


科目:初中数学 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下 5 个项目可供选择:径赛项目:100m、200m、1000m(分别用 A1、A2、A3 表示);田赛项目:跳远,跳高(分别用 T1、T2 表示).
(1)该同学从 5 个项目中任选一个,恰好是田赛项目的概率 P 为 ;
(2)该同学从 5 个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率 P1,利用列表法或树状图加以说明;
(3)该同学从 5 个项目中任选两个,则两个项目都是径赛项目的概率 P2 为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
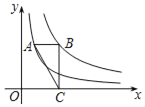
【题目】如图,点A在反比例函数y=![]() (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=![]() (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
(x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
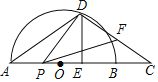
【题目】如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.
(1)求AD的长.
(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
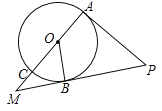
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年杭州市推出了“微公交”,“微公交”是国内首创的纯电动汽车租赁服务.它作为一种绿色出行方式,对缓解交通堵塞和停车困难,改善城市大气环境,都可以起到积极作用.据了解某租赁点拥有“微公交”![]() 辆.据统计,当每辆车的年租金为
辆.据统计,当每辆车的年租金为![]() 千元时可全部租出;每辆车的年租金每增加
千元时可全部租出;每辆车的年租金每增加![]() 千元,未租出的车将增加
千元,未租出的车将增加![]() 辆.
辆.
(1)当每辆车的年租金定为![]() 千元时,能租出多少辆?
千元时,能租出多少辆?
(2)当每辆车的年租金增加多少千元时,租赁公司的年收益(不计车辆维护等其他费用)可达到![]() 千元?
千元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别是AB,BC边上的点,且DE∥AC,若![]() ,
,![]() ,则△ACD的面积为( )
,则△ACD的面积为( )
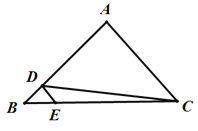
A. 64 B. 72 C. 80 D. 96
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借一段墙体(墙体的最大可用长度a=10m),设AB的长为xm,所围的花圃面积为ym2,则y的最大值是__________.
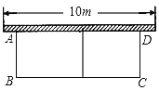
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com