
【题目】已知E,F分别是AB、CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD; 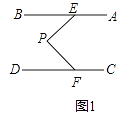
(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD; 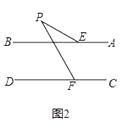
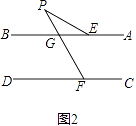
(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求 ![]() 的值.
的值. 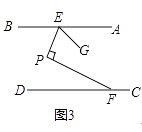
【答案】
(1)解:过P作PQ∥AB,

∵AB∥CD,
∴PQ∥CD,
∴∠BEP=∠1,∠2=∠PFD,
∵∠EPF=∠1+∠2,
∴∠EPF=∠BEP+∠PFD
(2)证明:∵∠BGP是△PEG的外角,
∴∠P=∠BGP﹣∠BEP.
∵∠P=∠PGB﹣∠BEP,
∴∠PFD=∠PGB,
∴AB∥CD
(3)解:由(1)的结论∠EPF=∠BEP+∠PFD=90°,
设∠PFD=x,则∠BEP=90°﹣x,
∵∠PEG=∠BEP=90°﹣x,
∴∠AEG=180°﹣2(90°﹣x)=2x,则 ![]() =
= ![]() =2
=2
【解析】(1)过P作PQ平行于AB,由AB与CD平行,得到PQ与CD平行,利用两直线平行内错角相等得到两对角相等,再由∠EPF=∠1+∠2,等量代换就可得证;(2)先根据三角形外角的性质得出∠P=∠BGP﹣∠BEP,再由∠P=∠PGB﹣∠BEP可知,∠PFD=∠PGB,由此可得出结论;(3)由(1)中的结论∠EPF=∠BEP+∠PFD,设设∠PFD=x,则∠BEP=90°﹣x,根据∠PEG=∠BEP=90°﹣x,利用平角定义表示出∠AEG,即可求出所求比值.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B,∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( ) 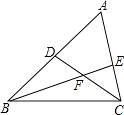
A.118°
B.119°
C.120°
D.121°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查6个人中2个人生肖相同的概率,进行有放回地摸球试验,则( )
A. 用12个球每摸6次为一次试验,看是否有2次相同
B. 用12个球每摸12次为一次试验,看是否有2次相同
C. 用6个球每摸12次为一次试验,看是否有2次相同
D. 用6个球每摸6次为一次试验,看是否有2次相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将平行四边形ABCD旋转到平行四边形A′B′C′D′的位置,下列结论错误的是( )
A. AB=A′B′ B. AB∥A′B′ C. ∠A=∠A′ D. △ABC≌△A′B′C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
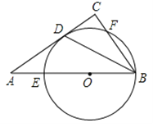
(1) 求证:AC是⊙O的切线;
(2) 已知AB=10,BC=6,求⊙O的半径r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com