
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
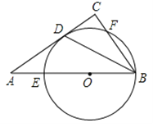
(1) 求证:AC是⊙O的切线;
(2) 已知AB=10,BC=6,求⊙O的半径r.
【答案】(1)证明参见解析;(2)![]() .
.
【解析】
试题分析:(1)连半径OD证垂直即可,利用BD平分∠ABC,OD=OB,可以推出∠ODB=∠DBC.得到OD∥BC,又因为∠C = 90°,所以∠ADO = 90°,从而得出结论;(2)因为OD∥BC,所以△AOD∽△ABC.得出对应线段成比例,即![]() ,代入数据得
,代入数据得![]() ,于是求出半径r.
,于是求出半径r.
试题解析:(1)连接OD. ∵OB=OD,∴∠OBD=∠ODB.∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ODB=∠DBC.∴OD∥BC,又∵∠C = 90°,∴∠ADO = 90°.∴AC⊥OD,即AC是⊙O的切线;(2)由(1)知,OD∥BC,∴△AOD∽△ABC.∴![]() ,即
,即![]() .解得
.解得![]() ,即⊙O的半径r为
,即⊙O的半径r为![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的关系,并说明你的结论. 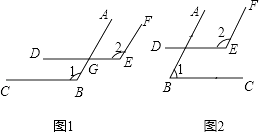
(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是: , 理由:;
(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是: , 理由: .
(3)由(1)(2)你得出的结论是:如果 , 那么 .
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角度数的分别是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别是AB、CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD; 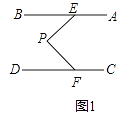
(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD; 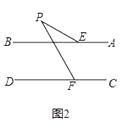
(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求 ![]() 的值.
的值. 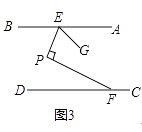
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一副三角板按如图所示的方式放置,则下列结论不正确的是( ) 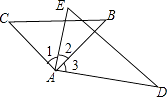
A.∠1=∠3
B.如果∠2=30°,则有AC∥DE
C.如果∠2=30°,则有BC∥AD
D.如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动手操作: 如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题: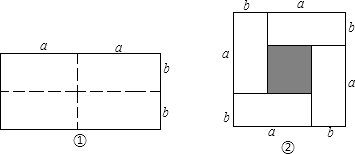
(1)观察图②,请用两种不同的方法表示阴影部分的面积;
(2)请写出三个代数式(a+b)2 , (a﹣b)2 , ab之间的一个等量关系. 问题解决:
根据上述(2)中得到的等量关系,解决下列问题:
已知:x+y=6,xy=3.求:(x﹣y)2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com