
分析 (1)直接利用有理数的乘除运算法则计算得出答案;
(2)直接利用有理数的乘方运算法则以及绝对值、有理数混合运算法则分别计算得出答案;
(3)直接利用度分秒的转换法则计算得出答案.
解答 解:(1)-2×(-3)+(-48)÷6
=6-8
=-2;
(2)-32+(-$\frac{5}{2}$)2×(-$\frac{4}{25}$)+|-22|+(-1)2013
=-9-1+4-1
=-7;
(3)12°24′27″×4-30°27′8″
=48°96′108″-30°27′8″
=18°69′100″
=19′10′40″.
点评 此题主要考查了有理数的混合运算法则以及度分秒的转换,正确把握运算法则是解题关键.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:解答题
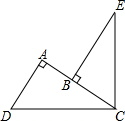 如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为点A、B.
如图,∠DCE=90°,CD=CE,DA⊥AC,EB⊥AC,垂足分别为点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
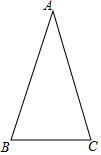 如图,△ABC是等腰三角形,AB=AC,∠A=36°.
如图,△ABC是等腰三角形,AB=AC,∠A=36°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com