
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G. 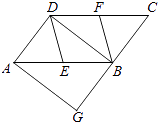
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE= ![]() AB,DF=
AB,DF= ![]() CD.
CD.
∴BE=DF,BE∥DF,
∴四边形DFBE是平行四边形,
∴DE∥BF
(2)证明:∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DFBE是平行四边形,
∴四边形DEBF是菱形
【解析】(1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,即可证明DE∥BF,(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.


科目:初中数学 来源: 题型:
【题目】5月19日为中国旅游日,衢州推出“读万卷书,行万里路,游衢州景”的主题系列旅游惠民活动,市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点;下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩,则王先生恰好上午选中孔氏南宗家庙,下午选中江郎山这两个地的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线l1 , l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2 , 经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.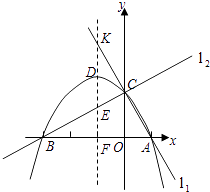
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1 , 抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮在学习探索三角形全等时,碰到如下一题:如图①,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?

(1)请你帮他们解答,并说明理由;
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE,DE,则有CE=DE,你知道为什么吗(如图②)?
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有(2)中类似的结论.请你帮他在图③中画出图形,并写出结论,不要求说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A的坐标为(﹣2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.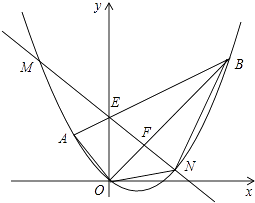
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当点F在线段OB上运动时,求△BON面积的最大值,并求出此时点N的坐标;
(4)连接AN,当△BON面积最大时,在坐标平面内求使得△BOP与△OAN相似(点B、O、P分别与点O、A、N对应)的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠A是锐角,则下列结论正确个数为( )个.
①![]() =sinA-1;②sinA+cosA>1;③tanA>sinA;④cosA=sin(90°﹣∠A)
=sinA-1;②sinA+cosA>1;③tanA>sinA;④cosA=sin(90°﹣∠A)
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装销售店到生产厂家选购A、B两种品牌的服装,若购进A品牌服装3套,B品牌服装4套,共需600元;若购进A品牌服装2套,B品牌服装3套,共需425元.
(1)求A、B两种品牌的服装每套进价分别为多少元?
(2)若A品牌服装每套售价为130元,B品牌服装每套售价为100元,根据市场的需求,现决定购进B品牌服装数量比A品牌服装数量的2倍还多3套.如果购进B品牌服装数量不多于39套,这样服装全部售出后,就能使获利总额不少于1335元,问共有几种进货方案?如何进货?(注:利润=售价-进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com