
【题目】计算
(1)27﹣16+(﹣7)﹣18;
(2)(﹣6)×(﹣![]() )÷(﹣
)÷(﹣![]() );
);
(3)(![]() ﹣
﹣![]() ﹣
﹣![]() )×60;
)×60;
(4)﹣24+3×(﹣1)4﹣(﹣2)3.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
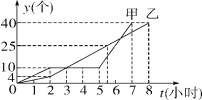
【题目】某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的关系如图所示.
(1)根据图象回答:
①甲、乙中,谁先完成一天的生产任务;在生产过程中,谁因机器故障停止生产多少小时;
②当t等于多少时,甲、乙所生产的零件个数相等;
(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.
(1)求证:①△OAC≌△OBD,②∠AEB=60°;
(2)连结OE,OE是否平分∠AED?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G. 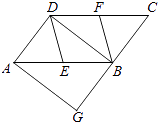
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义新运算“△”,对于任意有理数a,b,都有a△b=a2-ab+b,例如:3△5=32-3×5+5=-1,请根据上述知识解决问题:
(1)化简:(x-1)△(2+x);
(2)若(1)中的代数式的值大于6而小于9,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图1,将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax2+bx+c(a<0)过矩形顶点B、C. 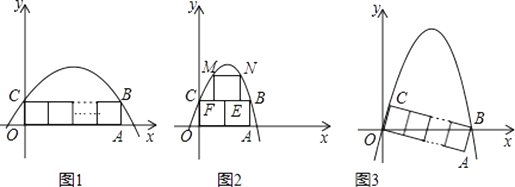
(1)当n=1时,如果a=﹣1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上,如果该抛物线同时经过原点O. ①试求当n=3时a的值;
②直接写出a关于n的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com