
【题目】如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.
(1)求证:①△OAC≌△OBD,②∠AEB=60°;
(2)连结OE,OE是否平分∠AED?请说明理由.

【答案】(1)求证:①详见解析;②详见解析;(2)OE平分∠AED,理由详见解析.
【解析】
(1)①根据SAS即可判定.②由△OAC≌OBD,推出∠OAE=∠OBD,由△OAB是等边三角形,推出∠OAB+∠OBA=120°,推出∠OAE+∠BAE+∠OBA=120°,即∠EAB+∠EBA=120°,推出∠AEB=60°.
(2)OE平分∠AED.作OM⊥AC于M,ON⊥BD于N.由△OAC≌△OBD,推出S△OAC=S△OBD,推出![]() ACOM=
ACOM=![]() BDON,推出OM=ON,再根据角平分线判定定理即可证明.
BDON,推出OM=ON,再根据角平分线判定定理即可证明.
(1)证明:①∵△OAB与△OCD都是等边三角形,
∴OA=OB,OC=OD,∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
∴△OAC≌△OBD.
②∵△OAC≌OBD,
∴∠OAE=∠OBD,
∵△OAB是等边三角形,
∴∠OAB+∠OBA=120°,
∴∠OAE+∠BAE+∠OBA=120°,
即∠EAB+∠EBA=120°,
∴∠AEB=60°.
(2)解:OE平分∠AED.理由如下:
作OM⊥AC于M,ON⊥BD于N.
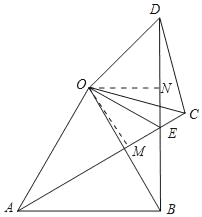
∵△OAC≌△OBD,
∴S△OAC=S△OBD,
∴![]() ACOM=
ACOM=![]() BDON,
BDON,
∴OM=ON,
∴OE平分∠AED.


科目:初中数学 来源: 题型:
【题目】在如下三个函数图象中,有两个函数图象能近似地刻画如下![]() 两个情境:
两个情境:
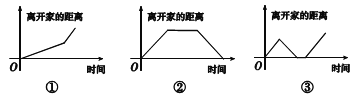
情境![]() :小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
情境![]() :小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境![]() ,
, ![]() 所对应的函数图象分别为 , (填写序号).
所对应的函数图象分别为 , (填写序号).
(2)请你为剩下的函数图象写出一个适合的情境.
查看答案和解析>>
科目:初中数学 来源: 题型:
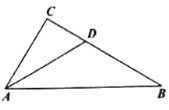
【题目】如图,∠CAB+∠ABC=90°,AD平分∠CAB,与BC边交于点D,BE平分∠ABC与AC边交于点E。
(1)依题意补全图形,并猜想∠DAB+∠EBA的度数等于__________;
(2)证明以上结论。
证明:∵ AD平分∠CAB,BE平分∠ABC,
∴∠DAB=![]() ∠CAB,
∠CAB,
∠EBA=__________.
(理由:____________________)
∵∠CAB+∠ABC=90°,
∴∠DAB+∠EBA=______×(∠______+∠______)=______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是两棵大树,两棵大树之间有一个废弃的圆形坑塘,为开发利用这个坑塘,需要测量A,B之间的距离,但坑塘附近地形复杂不容易直接测量.
(1)请你利用所学知识,设计一个测量A,B之间的距离的方案,并说明理由;
(2)在你设计的测量方案中,需要测量哪些数据?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示. 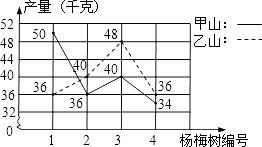
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的灰、白两种正方形地砖铺设地面,方法是(如图):第一层只有2块白色地砖,第二层是在第一层外面围一圈灰色地砖,第三层是在第二层外面围一圈白色地砖……
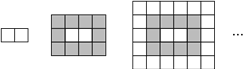
(1)第七层共有几块地砖,是白色的还是灰色的?
(2)第n层共有几块地砖(结果化成最简)?如果这些地砖是白色的,那么正整数n有什么特点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com