
”¾ĢāÄæ”æĪŖĮĖæ¼²ģ¼×”¢ŅŅĮ½ÖÖ³ÉŹģĘŚŠ”ĀóµÄÖźøß³¤ŹĘĒéæö£¬ĻÖ“ÓÖŠĖ껜³éČ”6Öź£¬²¢²āµĆĖüĆĒµÄÖźøߣص„Ī»£ŗcm£©ČēĻĀ±ķĖłŹ¾£ŗ
¼× | 63 | 66 | 63 | 61 | 64 | 61 |
ŅŅ | 63 | 65 | 60 | 63 | 64 | 63 |
£Ø¢ń£©Ēė·Ö±š¼ĘĖć±ķÄŚĮ½×鏿¾ŻµÄ·½²ī£¬²¢½č“Ė±Č½ĻÄÄÖÖŠ”ĀóµÄÖźøß³¤ŹĘ±Č½ĻÕūĘė£æ
£Ø¢ņ£©ĻÖ½«½ųŠŠĮ½ÖÖŠ”ĀóÓÅĮ¼Ę·ÖÖŌÓ½»ŹµŃ飬Šč“Ó±ķÄŚµÄ¼×”¢ŅŅĮ½ÖÖŠ”ĀóÖŠ£¬ø÷Ė껜³éČ”Ņ»Öź½ųŠŠÅä¶Ō£¬ŅŌŌ¤¹ĄÕūĢåÅä¶ŌĒéæö£¬ĒėÄćÓĆĮŠ±ķ·Ø»ņ»Ź÷דĶ¼µÄ·½·Ø£¬ĒóĖł³éČ”µÄĮ½ÖźÅä¶ŌŠ”ĀóÖźøßĒ”ŗƶ¼µČÓŚø÷×ŌĘ½¾łÖźøßµÄøÅĀŹ£®
”¾“š°ø”æ½ā£ŗ£Ø¢ń£©”ß ![]() =
= ![]() =63£¬ ”ąs¼×2=
=63£¬ ”ąs¼×2= ![]() ”Į[£Ø63©63£©2”Į2+£Ø66©63£©2+2”Į£Ø61©63£©2+£Ø64©63£©2]=3£»
”Į[£Ø63©63£©2”Į2+£Ø66©63£©2+2”Į£Ø61©63£©2+£Ø64©63£©2]=3£»
ӧ ![]() =
= ![]() =63£¬
=63£¬
”ąsŅŅ2= ![]() ”Į[£Ø63©63£©2”Į3+£Ø65©63£©2+£Ø60©63£©2+£Ø64©63£©2]=
”Į[£Ø63©63£©2”Į3+£Ø65©63£©2+£Ø60©63£©2+£Ø64©63£©2]= ![]() £¬
£¬
”ßsŅŅ2£¼s¼×2 £¬
”ąŅŅÖÖŠ”ĀóµÄÖźøß³¤ŹĘ±Č½ĻÕūĘė£»
£Ø¢ņ£©ĮŠ±ķČēĻĀ£ŗ
63 | 66 | 63 | 61 | 64 | 61 | |
63 | 63Ӣ63 | 66Ӣ63 | 63Ӣ63 | 61Ӣ63 | 64Ӣ63 | 61Ӣ63 |
65 | 63Ӣ65 | 66Ӣ65 | 63Ӣ65 | 61Ӣ65 | 64Ӣ65 | 61Ӣ65 |
60 | 63Ӣ60 | 66Ӣ60 | 63Ӣ60 | 61Ӣ60 | 64Ӣ60 | 61Ӣ60 |
63 | 63Ӣ63 | 66Ӣ63 | 63Ӣ63 | 61Ӣ63 | 64Ӣ63 | 61Ӣ63 |
64 | 63Ӣ64 | 66Ӣ64 | 63Ӣ64 | 61Ӣ64 | 64Ӣ64 | 61Ӣ64 |
63 | 63Ӣ63 | 66Ӣ63 | 63Ӣ63 | 61Ӣ63 | 64Ӣ63 | 61Ӣ63 |
ÓɱķøńæÉÖŖ£¬¹²ÓŠ36ÖÖµČæÉÄܽį¹ū£¬ĘäÖŠĮ½ÖźÅä¶ŌŠ”ĀóÖźøßĒ”ŗƶ¼µČÓŚø÷×ŌĘ½¾łÖźøßµÄÓŠ6ÖÖ£¬
”ąĖł³éČ”µÄĮ½ÖźÅä¶ŌŠ”ĀóÖźøßĒ”ŗƶ¼µČÓŚø÷×ŌĘ½¾łÖźøßµÄøÅĀŹĪŖ ![]() =
= ![]() £®
£®
”¾½āĪö”æ£Ø¢ń£©ĻČ¼ĘĖć³öĘ½¾łŹż£¬ŌŁŅĄ¾Ż·½²ī¹«Ź½¼“æÉµĆ£» £Ø¢ņ£©ĮŠ±ķµĆ³öĖłÓŠµČæÉÄܽį¹ū£¬ÓɱķøńµĆ³öĮ½ÖźÅä¶ŌŠ”ĀóÖźøßĒ”ŗƶ¼µČÓŚø÷×ŌĘ½¾łÖźøߵĽį¹ūŹż£¬ŅĄ¾ŻøÅĀŹ¹«Ź½Ēó½āæÉµĆ£®
”¾æ¼µć¾«Īö”æ¹ŲÓŚ±¾Ģāæ¼²éµÄĮŠ±ķ·ØÓėŹ÷דĶ¼·Ø£¬ŠčŅŖĮĖ½āµ±Ņ»“ĪŹŌŃéŅŖÉč¼ĘČżøö»ņøü¶ąµÄŅņĖŲŹ±£¬ÓĆĮŠ±ķ·Ø¾Ķ²»·½±ćĮĖ£¬ĪŖĮĖ²»ÖŲ²»Ā©µŲĮŠ³öĖłÓŠæÉÄܵĽį¹ū£¬Ķس£²ÉÓĆŹ÷דĶ¼·ØĒóøÅĀŹ²ÅÄÜµĆ³öÕżČ·“š°ø£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£ŗÖ±ĻßAB¾¹żµćA£Ø0£¬3£©µćB£Ø ![]() £¬0£©£¬µćMŌŚyÖįÉĻ£¬”ŃM¾¹żµćA”¢B£¬½»xÖįÓŚĮķŅ»µćC£®
£¬0£©£¬µćMŌŚyÖįÉĻ£¬”ŃM¾¹żµćA”¢B£¬½»xÖįÓŚĮķŅ»µćC£® 
£Ø1£©ĒóÖ±ĻßABµÄ½āĪöŹ½£»
£Ø2£©ĒóµćMµÄ×ų±ź£»
£Ø3£©µćPŹĒĮÓ»”ACÉĻŅ»øö¶Æµć£¬µ±PµćŌĖ¶ÆŹ±£¬ĪŹ£ŗĻ߶ĪPA£¬PB£¬PCÓŠŹ²Ć“ŹżĮæ¹ŲĻµ£æ²¢øų³öÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDµÄ±ß³¤ĪŖ5£¬µćAµÄ×ų±źĪŖ£Ø©4£¬0£©£¬µćBŌŚyÖįÉĻ£¬Čō·“±ČĄżŗÆŹż![]() £Øk”Ł0£©µÄĶ¼Ļó¹żµćC£¬ŌņøĆ·“±ČĄżŗÆŹżµÄ±ķ“ļŹ½ĪŖ£Ø””””£©
£Øk”Ł0£©µÄĶ¼Ļó¹żµćC£¬ŌņøĆ·“±ČĄżŗÆŹżµÄ±ķ“ļŹ½ĪŖ£Ø””””£©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷ĪŖĮĖĮĖ½āĘųĪĀ¶ŌÓƵēĮæµÄÓ°Ļģ£¬¶ŌČ„Äź×Ō¼ŗ¼ŅµÄĆæŌĀÓƵēĮæŗĶµ±µŲĘųĪĀ½ųŠŠĮĖĶ³¼Ę£®µ±µŲČ„ÄźĆæŌĀµÄĘ½¾łĘųĪĀČēĶ¼1£¬Š”Ć÷¼ŅČ„ÄźŌĀÓƵēĮæČēĶ¼2£®
øł¾ŻĶ³¼Ę±ķ£¬»Ų“šĪŹĢā£ŗ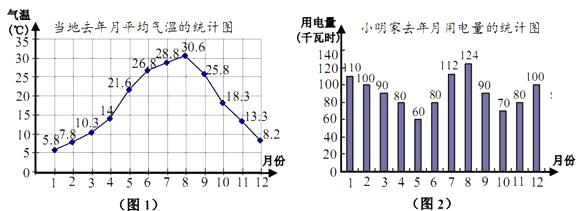
£Ø1£©µ±µŲČ„ÄźŌĀĘ½¾łĘųĪĀµÄ×īøßÖµ”¢×īµĶÖµø÷ĪŖ¶ąÉŁ£æĻąÓ¦ŌĀ·ŻµÄÓƵēĮæø÷ŹĒ¶ąÉŁ£æ
£Ø2£©Ēė¼ņµ„ĆčŹöŌĀÓƵēĮæÓėĘųĪĀÖ®¼äµÄ¹ŲĻµ£»
£Ø3£©¼ŁÉčČ„ÄźŠ”Ć÷¼ŅÓƵēĮæŹĒĖłŌŚÉēĒų¼ŅĶ„ÄźÓƵēĮæµÄÖŠĪ»Źż£¬¾Ż“ĖĖūÄÜ·ńŌ¤²ā½ńÄźøĆÉēĒųµÄÄźÓƵēĮæ£æĒė¼ņŅŖĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćPĪŖ¶Ø½Ē”ĻAOBµÄĘ½·ÖĻßÉĻµÄŅ»øö¶Øµć£¬ĒŅ”ĻMPNÓė”ĻAOB»„²¹£¬Čō”ĻMPNŌŚČʵćPŠż×ŖµÄ¹ż³ĢÖŠ£¬ĘäĮ½±ß·Ö±šÓėOA”¢OBĻą½»ÓŚM”¢NĮ½µć£¬ŌņŅŌĻĀ½įĀŪ£ŗ£Ø1£©PM=PNŗć³ÉĮ¢£»£Ø2£©OM+ONµÄÖµ²»±ä£»£Ø3£©ĖıߊĪPMONµÄĆ껿²»±ä£»£Ø4£©MNµÄ³¤²»±ä£¬ĘäÖŠÕżČ·µÄøöŹżĪŖ£Ø £© 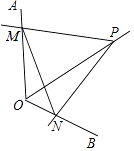
A.4
B.3
C.2
D.1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ķ¼ÖŠÓė”ĻEŹĒĶ¬Ī»½ĒµÄÓŠ_________________£¬Óė”ĻDŹĒÄŚ“ķ½ĒµÄÓŠ________________£¬Óė”ĻEŹĒĶ¬ÅŌÄŚ½ĒµÄÓŠ______________________£¬Óė”ĻDŹĒĶ¬ÅŌÄŚ½ĒµÄÓŠ_______________.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Õż·½ŠĪ![]() µÄ¶„µć
µÄ¶„µć![]() Óė×ų±źŌµćÖŲŗĻ£¬Ęä±ß³¤ĪŖ2£¬µć
Óė×ų±źŌµćÖŲŗĻ£¬Ęä±ß³¤ĪŖ2£¬µć![]() £¬µć
£¬µć![]() ·Ö±šŌŚ
·Ö±šŌŚ![]() Öį£¬
Öį£¬ ![]() ÖįµÄÕż°ėÖįÉĻ.ŗÆŹż
ÖįµÄÕż°ėÖįÉĻ.ŗÆŹż![]() µÄĶ¼ĻńÓė
µÄĶ¼ĻńÓė![]() ½»ÓŚµć
½»ÓŚµć![]() £¬ŗÆŹż
£¬ŗÆŹż![]() ĪŖ³£Źż£¬
ĪŖ³£Źż£¬ ![]() )µÄĶ¼Ļń¾¹żµć
)µÄĶ¼Ļń¾¹żµć![]() £¬Óė
£¬Óė![]() ½»ÓŚµć
½»ÓŚµć![]() £¬ÓėŗÆŹż
£¬ÓėŗÆŹż![]() µÄĶ¼ĻńŌŚµŚČżĻó·žÄŚ½»ÓŚµć
µÄĶ¼ĻńŌŚµŚČżĻó·žÄŚ½»ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() .
.
(1)ĒóŗÆŹż![]() µÄ±ķ“ļŹ½£¬²¢Ö±½ÓŠ“³ö
µÄ±ķ“ļŹ½£¬²¢Ö±½ÓŠ“³ö![]() Į½µćµÄ×ų±ź;
Į½µćµÄ×ų±ź;
(2)Ēó![]() µÄĆ껿.
µÄĆ껿.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¼×”¢ŅŅĮ½“¬“ÓøŪæŚAĶ¬Ź±³ö·¢£¬¼×“¬ŅŌ30ŗ£Ąļ/Ź±µÄĖŁ¶ČĻņ±±Ę«¶«35”ćµÄ·½Ļņŗ½ŠŠ£¬ŅŅ“¬ŅŌ40ŗ£Ąļ/Ź±µÄĖŁ¶ČĻņĮķŅ»·½Ļņŗ½ŠŠ£¬2Š”Ź±ŗ󣬼ד¬µ½“ļCµŗ£¬ŅŅ“¬µ½“ļBµŗ£¬ČōC£¬BĮ½µŗĻą¾ą100ŗ£Ąļ£¬ŌņŅŅ“¬ŗ½ŠŠµÄ·½ĻņŹĒÄĻĘ«¶«¶ąÉŁ¶Č£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅĆĒŌĖÓĆĶ¼£Ø¢ń£©ÖŠ“óÕż·½ŠĪµÄĆ껿æɱķŹ¾ĪŖ£Øa+b£©2£¬Ņ²æɱķŹ¾ĪŖc3+4£Ø![]() ab£©£¬¼“£Øa+b£©2=c2+4£Ø
ab£©£¬¼“£Øa+b£©2=c2+4£Ø![]() ab£©ÓÉ“ĖĶʵ¼³öŅ»øöÖŲŅŖµÄ½įĀŪa2+b2=c2£¬ÕāøöÖŲŅŖµÄ½įĀŪ¾ĶŹĒÖųĆūµÄ”°¹“¹É¶ØĄķ”±£®ÕāÖÖøł¾ŻĶ¼ŠĪæÉŅŌ¼«¼ņµ„µŲÖ±¹ŪĶĘĀŪ»ņŃéÖ¤ŹżŃ§¹ęĀÉŗĶ¹«Ź½µÄ·½·Ø£¬¼ņ³Ę”°ĪŽ×ÖÖ¤Ć÷”±£®
ab£©ÓÉ“ĖĶʵ¼³öŅ»øöÖŲŅŖµÄ½įĀŪa2+b2=c2£¬ÕāøöÖŲŅŖµÄ½įĀŪ¾ĶŹĒÖųĆūµÄ”°¹“¹É¶ØĄķ”±£®ÕāÖÖøł¾ŻĶ¼ŠĪæÉŅŌ¼«¼ņµ„µŲÖ±¹ŪĶĘĀŪ»ņŃéÖ¤ŹżŃ§¹ęĀÉŗĶ¹«Ź½µÄ·½·Ø£¬¼ņ³Ę”°ĪŽ×ÖÖ¤Ć÷”±£®



£Ø1£©ĒėÄćÓĆĶ¼£Ø¢ņ£©£Ø2002Äź¹ś¼ŹŹżŃ§¼Ņ“ó»į»į±ź£©µÄĆ껿±ķ“ļŹ½ŃéÖ¤¹“¹É¶ØĄķ£ØĘäÖŠĖÄøöÖ±½ĒČż½ĒŠĪµÄ½Ļ“óµÄÖ±½Ē±ß³¤¶¼ĪŖa£¬½ĻŠ”µÄÖ±½Ē±ß³¤¶¼ĪŖb£¬Š±±ß³¤¶¼ĪŖc£©£®
£Ø2£©ĒėÄćÓĆ£Ø¢ó£©Ģį¹©µÄĶ¼ŠĪ½ųŠŠ×éŗĻ£¬ÓĆ×éŗĻĶ¼ŠĪµÄĆ껿±ķ“ļŹ½ŃéÖ¤£ŗ£Øx+2y£©2=x2+4xy+4y2£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com