
【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式. 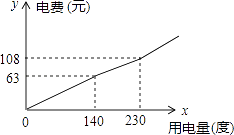
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费元;
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.
【答案】
(1)140<x≤230;x>230
(2)54
(3)解:设第二档每月电费y(元)与用电量x(度)之间的函数关系式为:y=ax+c,
将(140,63),(230,108)代入得出:
![]() ,
,
解得: 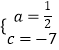 ,
,
则第二档每月电费y(元)与用电量x(度)之间的函数关系式为:y= ![]() x﹣7(140<x≤230)
x﹣7(140<x≤230)
(4)解:根据图象可得出:用电230度,需要付费108元,用电140度,需要付费63元,
故,108﹣63=45(元),230﹣140=90(度),
45÷90=0.5(元/度),
则第二档电费为0.5元/度;
∵小刚家某月用电290度,交电费153元,
290﹣230=60(度),153﹣108=45(元),
45÷60=0.75(元/度),
m=0.75﹣0.5=0.25,
答:m的值为0.25
【解析】解:(1)利用函数图象可以得出,阶梯电价方案分为三个档次,利用横坐标可得出: 第二档:140<x≤230,第三档x>230;
2)根据第一档范围是:0<x≤140,
根据图象上点的坐标得出:设解析式为:y=kx,将(140,63)代入得出:k= ![]() =0.45,
=0.45,
故y=0.45x,
当x=120,y=0.45×120=54(元),
所以答案是:54;


科目:初中数学 来源: 题型:
【题目】(1)﹣![]() a2bc+
a2bc+![]() cba2
cba2
(2)7ab﹣3a2b2+7+8ab2+3a2b2﹣3﹣7ab
(3)(﹣x+2x2+5)+(4x2﹣3﹣6x)
(4)(2x2﹣![]() +3x)﹣4(x﹣x2+
+3x)﹣4(x﹣x2+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣ ![]() 上,B、D在双曲线y2=
上,B、D在双曲线y2= ![]() 上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= . 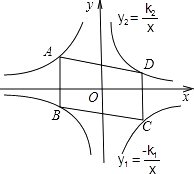
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牛奶厂在一条南北走向的大街上设有O,A,B,C四家特约经销店.A店位于O店的南面3千米处;B店位于O店的北面1千米处,C店在O店的北面2千米处.
(1)请以O为原点,向北的方向为正方向,1个单位长度表示1千米,画一条数轴,你能在数轴上分别表示出O,A,B,C的位置吗?
(2)牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店,那么送货车走的最短路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求铁架垂直管CE的长(结果精确到0.01米). 
查看答案和解析>>
科目:初中数学 来源: 题型:
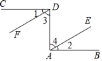
【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把证明过程补充完整.
证明:∵ ,
∴∠CDA=90°,∠DAB=90° ( ).
∴∠1+∠3=90°,∠2+∠4=90°.
又∵∠1=∠2,
∴ ( ),
∴DF∥AE ( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com