
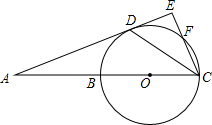
 如图,直线AD切⊙O于点D,直线AB经过圆心O,交⊙O于点B、C,CE⊥AD,垂足为E,CE交⊙O于点F,连接CD.
如图,直线AD切⊙O于点D,直线AB经过圆心O,交⊙O于点B、C,CE⊥AD,垂足为E,CE交⊙O于点F,连接CD.分析 (1)$\widehat{BD}$=$\widehat{FD}$,连接OD,由切线的性质和已知条件证明圆周角∠OCD=∠DCE即可;
(2)连接BD,易求CD的长,再由相等的角则其三角函数值也相等可求出sin∠DCB的值,进而可得到直径BC的长,圆的半径也就求出.
解答 解:(1)$\widehat{BD}$=$\widehat{FD}$,理由如下:
连接OD,
∵直线AD切⊙O于点D,
∴OD⊥AE,
∵CE⊥AD,垂足为E,
∴OD∥CE,
∴∠ODC=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∴∠OCD=∠DCE,
∴$\widehat{BD}$=$\widehat{FD}$; (2)连接BD,
(2)连接BD,
∵sin∠DCE=$\frac{3}{5}$,
∴$\frac{DE}{CD}=\frac{3}{5}$,
∵CE=8,∠E=90°,
∴CD=10,
∵∠OCD=∠DCE,
∴sin∠DCB=$\frac{3}{5}$,
∴$\frac{DC}{BC}=\frac{4}{5}$,
∴BC=$\frac{25}{2}$,
∴⊙O的半径=$\frac{25}{4}$.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:解答题
 如图所示.
如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④△>0;⑤4a-2b+c<0,其中正确的个数为( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④△>0;⑤4a-2b+c<0,其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$
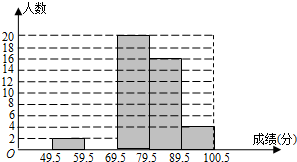
(1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com