【题目】生活与应用：
在一条笔直的东西走向的马路上，有少年宫、学校、超市、医院四家公共场所．已知少年宫在学校东300米，超市在学校西200米，医院在学校东500米．
（1）你能利用所学过的数轴知识描述它们的位置吗？
（2）小明放学后要去医院看望生病住院的奶奶，他从学校出发向西走了200米，又向西走了﹣700米，你说他能到医院吗？
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目：初中数学 来源： 题型：
【题目】已知二次函数的图象经过点（0，﹣3），顶点坐标为（﹣1，﹣4），
（1）求这个二次函数的解析式；
（2）求图象与x轴交点A、B两点的坐标；
（3）图象与y轴交点为点C，求三角形ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列三行数：
－3，9，－27，81，－243，….
－5，7，－29，79，－245，….
－1，3，－9，27，－81，….
(1)第一行数是按什么规律排列的？
(2)第二行、第三行数与第一行数分别有什么关系？
(3)分别取这三行数中的第6个数，计算这三个数的和．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算正确的是( )
A. 2÷
×
＝2÷1＝2 B. －24＋22÷20＝－24＋4÷20＝－20÷20＝－1
C. 
－2×(
－
)＝－2×(－
)＝＋＝
D. －12÷(6×3)＝－2×3＝－6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=12，DC=14，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与 CD1交于点O，则线段AD1的长为（ ）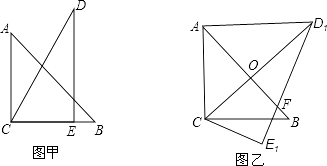 
A.6 
B.10
C.8
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，D是BC上任意一点，过D分别向AB、AC引垂线，垂足分别为E、F点．
（1）当点D在BC的什么位置时，DE=DF？并证明．
（2）在满足第一问的条件下，连接AD，此时图中共有几对全等三角形？并请给予写出（不 必证明）．
（3）过C点作AB边上的高CG，请问DE、DF、CG的长之间存在怎样的等量关系？并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的，如果规定向东为正，向西为负，他这天下午行驶里程如下：（单位：千米）
+15, -3, +14，-11，+10，-12，+4，-15，+16，-18
（1）他将最后一名乘客送到目的地时，距下午出车地点是多少千米？
（2）若汽车耗油量为
升∕千米，这天下午共耗油多少升
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2，求证：CD⊥AB．
证明：∵DG⊥BC，AC⊥BC（已知）
∴∠DGB=∠ACB=90°（垂直定义）
∴DG∥AC（ ）
∴∠2= （ ）
∵∠1=∠2（已知）
∴∠1=∠ （等量代换）
∴EF∥CD（ ）
∴∠AEF=∠ （ ）
∵EF⊥AB（已知）
∴∠AEF=90°（ ）
∴∠ADC=90°（ ）
∴CD⊥AB（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线AB与函数y＝
（x＞0）的图象交于点A（m，2），B（2，n）．过点A作AC平行于x轴交y轴于点C，在y轴负半轴上取一点D，使OD＝
OC，且△ACD的面积是6，连接BC．
（1）求m，k，n的值；
（2）求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
