
【题目】如图,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等边三角形(点A、C、P按逆时针方向排列);当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合)


初步探究
(1)写出点B的坐标 ;
(2)点C在x轴上移动过程中,当等边三角形ACP的顶点P在第三象限时,连接BP,求证:△AOC≌△ABP.
深入探究
(3)当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论;
拓展应用
(4)点C在x轴上移动过程中,当△POB为等腰三角形时,直接写出此时点C的坐标.
【答案】(1)(![]() ,1);(2)证明见解析;(3)点P在过点B且垂直于AB的直线上; (4)点C的坐标为:(2,0)或(-
,1);(2)证明见解析;(3)点P在过点B且垂直于AB的直线上; (4)点C的坐标为:(2,0)或(-![]() ,0)或(-2,0)或C(-2
,0)或(-2,0)或C(-2![]() ,0).
,0).
【解析】
(1)如图1中,作BH⊥OA于H,利用等边三角形的性质,解直角三角形求出BH、OH即可得答案;
(2)由等边三角形的性质可得AO=AB,AC=AP,∠CAP=∠OAB=60°,继而可得∠CAO=∠PAB,利用SAS即可得证;
(3)由△AOC≌△ABP,可得∠ABP=∠AOC=90°,继而可得 点P在过点B且垂直于AB的直线上;
(4)分4种情况,①点C在x轴正半轴上,点P在第一象限时,BP=OB;②点C在x轴负半轴,点P在x轴正半轴时,OP=BP;③点C在x轴负半轴,点P在第四象限时,BP=OB;④点C在x轴负半轴,点P在y轴负半轴,针对四种情况分别画出图形并求解即可得.
(1)如图1中,作BH ⊥OA于H,
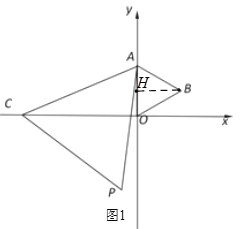
∵A(0,2),
∴OA=2,
∵△AOB是等边三角形,
∴OA=OB=AB=2,∠BOH=60°,
在Rt△OBH中,OH=AH=1,BH=![]() =
=![]() ,
,
∴B(![]() ,1);
,1);
(2)如图2,
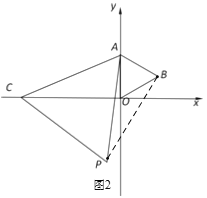
∵△AOB与△ACP都是等边三角形,
∴AO=AB,AC=AP,∠CAP=∠OAB=60°,
∴∠CAP+∠PAO=∠OAB+∠PAO,
即∠CAO=∠PAB,
∴△AOC≌△ABP(SAS);
(3)如图2中,∵△AOC≌△ABP,
∴∠ABP=∠AOC=90°,
∴PB⊥AB,
∴点P在过点B且垂直于AB的直线上;
(4)①如图3,当点C在x轴正半轴上,点P在第一象限时,BP=OB=2,

∵∠ABP=90°,
∴AP=![]() =2
=2![]() ,
,
∴AC=AP=2![]() ,
,
∴OC=![]() ,
,
∴C(2,0);
②如图4,当点C在x轴负半轴,点P在x轴正半轴时,OP=BP,此时AP垂直平分OB,
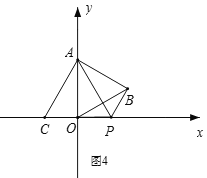
∴∠OAP=30°,
∴AP=PC=2OP,
∵AO2+OP2=AP2,即22+OP2=4OP2,
∴OP=![]() ,
,
∴OC=![]() ,
,
∴C(-![]() ,0);
,0);
③如图5,当点C在x轴负半轴,点P在第四象限时,BP=OB=2,
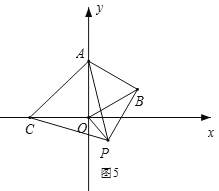
∵∠ABP=90°,
∴AP=![]() =2
=2![]() ,
,
∴AC=AP=2![]() ,
,
∴OC=![]() ,
,
∴C(-2,0);
④如图6,当点C在x轴负半轴,点P在y轴负半轴时,OP=OB=2,
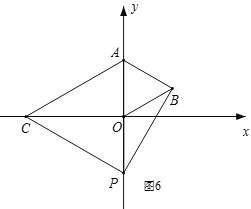
此时AP=2OP=4,∴AC=AP=4,
∵∠AOC=90°,OA=2,
∴OC=![]() ,
,
∴C(-2![]() ,0);
,0);
综上,点C的坐标为:(2,0)或(-![]() ,0)或(-2,0)或C(-2
,0)或(-2,0)或C(-2![]() ,0).
,0).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣![]() ,y=
,y=![]() 的图象交于B、A两点,则tan∠OAB的值的变化趋势为( )
的图象交于B、A两点,则tan∠OAB的值的变化趋势为( )
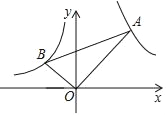
A. 逐渐变小 B. 逐渐变大 C. 时大时小 D. 保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.

(1)利用尺规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若AB=5,AC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为矩形,AD=20cm、AB=10cm.M点从D到A,P点从B到C,两点的速度都为2cm/s;N点从A到B,Q点从C到D,两点的速度都为1cm/s.若四个点同时出发.
(1)判断四边形MNPQ的形状.
(2)四边形MNPQ能为菱形吗?若能,请求出此时运动的时间;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为![]() 米.
米.
(1)如果通道所占面积是整个长方形空地面积的![]() ,求出此时通道的宽;
,求出此时通道的宽;
(2)能否设计出符合题目要求,且长方形花圃的形状与原长方形空地的形状相似的花圃?若能,求出此时通道的宽;若不能,则说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=36°时,求∠DEF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com