
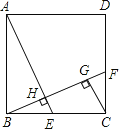
【题目】如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1) CG=BH;(2)FC2=BF·GF;(3)![]() .
.
【答案】(1)、 (2)、 (3) 证明见解析
【解析】
证明:(1)∵BF⊥AE,CG∥AE,CG⊥BF,∴CG⊥BF.
∵在正方形ABCD中,∠ABH+∠CBG=900, ∠CBG+∠BCG=900, ∠BAH+∠ABH=900,
∴∠BAH=∠CBG,∠ABH=∠BCG。
又∵AB=BC,∴△ABH≌△BCG(ASA)。∴CG=BH。
(2)∵∠BFC=∠CFG,∠BCF=∠CGF=900,∴△CFG∽△BFC。
∴![]() ,即FC2=BF·GF。
,即FC2=BF·GF。
(3)∵∠CBG=∠FBC,∠CGB=∠FCB =900,∴△CBG∽△FBC。
∴![]() ,即BC2=BF·BG。
,即BC2=BF·BG。
∵AB=BC,∴AB2=BF·BG。
∴![]() ,即
,即![]() 。
。
(1)由互余关系得出∠BAH=∠CBG,而∠AHB=∠BGC=90°,AB=BC,可证△ABH≌△BCG,得出结论。
(2)在Rt△BCF中,CG⊥BF,利用互余关系可证△CFG∽△BFC,利用相似比得出结论。
(3)根据Rt△BCF中,CG⊥BF,同理可证△CBG∽△FBC,利用相似比得出BC2=BF·BG,即AB2=BF·BG,结合(2)的结论求比即可。


科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一直角三角形两直角边分别为6![]() 、8
、8![]() ,在其外部拼上一个以8
,在其外部拼上一个以8![]() 为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是__________
为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,Rt△ABC中,∠ACB=90°,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,已知AB=3![]() ,BC=3
,BC=3![]() ,BE=5.求DE的长.
,BE=5.求DE的长.
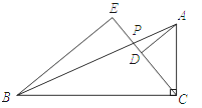
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() .直线
.直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
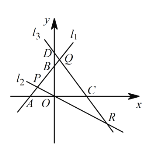
(1)点![]() 的坐标是 ,点
的坐标是 ,点![]() 的坐标是 ,点
的坐标是 ,点![]() 的坐标是 ;
的坐标是 ;
(2)将![]() 沿
沿![]() 轴折叠后,点
轴折叠后,点![]() 的对应点为
的对应点为![]() ,试判断点
,试判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
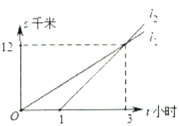
【题目】如图,![]() 两地相距
两地相距![]() 千米,甲、乙两人都从
千米,甲、乙两人都从![]() 地去
地去![]() 地,图中
地,图中![]() 和
和![]() 分别表示甲、乙两人所走路程
分别表示甲、乙两人所走路程![]() (千米)与时间
(千米)与时间![]() (小时)之间的关系,下列说法: ①乙晚出发
(小时)之间的关系,下列说法: ①乙晚出发![]() 小时;②乙出发
小时;②乙出发![]() 小时后追上甲;③甲的速度是
小时后追上甲;③甲的速度是![]() 千米/小时; ④乙先到达
千米/小时; ④乙先到达![]() 地.其中正确的是__________.(填序号)
地.其中正确的是__________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
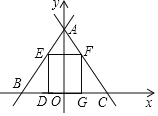
【题目】如图,直线y=kx+b与直线y=2x+6关于y轴对称且交于点A,直线y=2x+6交x轴于点B,直线y=kx+b交x轴于点C,正方形DEFG一边DG在线段BC上,点E在线段AB上,点F在线段AC上,则点G的坐标是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com