
【题目】有一直角三角形两直角边分别为6![]() 、8
、8![]() ,在其外部拼上一个以8
,在其外部拼上一个以8![]() 为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是__________
为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是__________![]() .
.
【答案】32或20+![]() 或
或![]()
【解析】
根据勾股定理求出斜边AB,(1)当AB=AD时,求出CD即可;(2)当AB=BD时,求出CD、AD即可;(3)当DA=DB时,设AD=x,则CD=x-6,求出即可.
如图1,在Rt△ABC中,
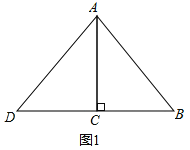
∵AC=8cm,BC=6cm,
∴AB=10cm,
(1)如图1所示:
当AB=AD=10cm时,CD=6cm,
△ABD的周长为10cm+10cm+6cm+6cm=32cm;
(2)如图2所示:
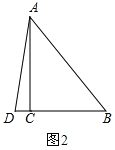
当AB=BD=10cm时,则CD=BD-BC=10-6=4(cm),
∴![]() (cm),
(cm),
△ABD的周长是10cm+10cm+![]() cm=(20+
cm=(20+![]() )cm;
)cm;
(3)当DA=DB时,如图2所示:
设![]() ,则
,则![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴△ABD的周长是10cm+![]() cm+
cm+![]() cm=
cm=![]() cm.
cm.
故答案为:32或20+![]() 或
或![]()


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB运动,速度为2cm/s;动点Q从点B开始沿BC运动,速度为4cm/s.设P、Q两点同时运动,运动时间为ts(0<t<4),当△QBP与△ABC相似时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
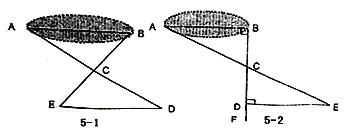
【题目】八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图5-1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图5-2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后1回答下列问题:
(1)方案(Ⅰ)是否可行?说明理由.
(2)方案(Ⅱ)是否可行?说明理由.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°, 方案(Ⅱ)是否成立? .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明元旦前到文具超市用15元买了若干练习本,元旦这一天,该超市开展优惠活动,同样的练习本比元旦前便宜0.2元,小明又用20.7元钱买练习本,所买练习本的数量比上一次多50%,小明元旦前在该超市买了多少本练习本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
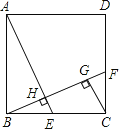
【题目】如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1) CG=BH;(2)FC2=BF·GF;(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
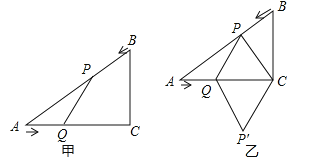
【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,如果点P从点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s,连接PQ,设运动时间为t(s)(0<t<4).
(1)当t为何值时,PQ∥BC;
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由;
(3)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com