
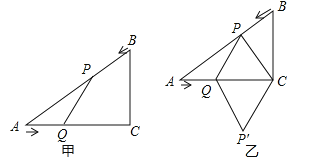
【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,如果点P从点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s,连接PQ,设运动时间为t(s)(0<t<4).
(1)当t为何值时,PQ∥BC;
(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由;
(3)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值.
【答案】(1)当t=![]() 秒,PQ∥BC;(2)不存在某时刻t,使线段PQ恰好把△ABC的面积平分;(3)当四边形PQP'C为菱形时,t的值为
秒,PQ∥BC;(2)不存在某时刻t,使线段PQ恰好把△ABC的面积平分;(3)当四边形PQP'C为菱形时,t的值为![]() 秒.
秒.
【解析】
(1)先根据勾股定理求得AB=5,由运动知,BP=t,得出AP=5﹣t,AQ=t,再得出![]() ,代入建立方程即可得出结论;
,代入建立方程即可得出结论;
(2)先求出S△AQP![]() S△ABC,再求出S△ABC=6,进而的粗S△AQP=3,再表示出PG
S△ABC,再求出S△ABC=6,进而的粗S△AQP=3,再表示出PG![]() (5﹣t),利用S△AQP
(5﹣t),利用S△AQP![]() t2
t2![]() t=3,建立方程,即可得出结论;
t=3,建立方程,即可得出结论;
(3)先判断出PE⊥AC,QE=EC,再判断出△APE∽△ABC,进而得出AE![]() t+4,QE=AE﹣AQ
t+4,QE=AE﹣AQ![]() t+4,建立方程即可得出结论.
t+4,建立方程即可得出结论.
在Rt△ABC中,AC=4,BC=3,根据勾股定理得:AB=5,
由运动知,BP=t,
∴AP=5﹣t,AQ=t.
∵PQ∥BC,
∴![]() ,
,
∴![]() ,
,
∴t![]() ,
,
∴当t![]() 秒,PQ∥BC;
秒,PQ∥BC;
(2)假设存在某时刻t,使线段PQ恰好把△ABC的面积平分,
∴S△AQP![]() S△ABC.
S△ABC.
∵S△ABC![]() ACBC=6,
ACBC=6,
∴S△AQP=3,过点P作PG⊥AC于G.
∵PG∥BC,
∴![]() ,
,
∴![]() ,
,
∴PG![]() (5﹣t),
(5﹣t),
∴S△AQP![]() AQPG
AQPG![]() t
t![]() (5﹣t)
(5﹣t)![]() t2
t2![]() t,
t,
∴![]() t2
t2![]() t=3,即:t2﹣5t+10=0.
t=3,即:t2﹣5t+10=0.
∵△=25﹣40=﹣15<0,
∴此方程无实数根,
∴不存在某时刻t,使线段PQ恰好把△ABC的面积平分;
(3)如图乙.连接PP',PP'交QC于E,当四边形PQP'C为菱形时,PE垂直平分QC,即:PE⊥AC,QE=EC.
∵∠ACB=90°,
∴PE∥BC,
∴△APE∽△ABC,
∴![]() ,
,
∴AE![]() t+4,QE=AE﹣AQ
t+4,QE=AE﹣AQ![]() t+4﹣t
t+4﹣t![]() t+4,
t+4,
∴![]() t+4
t+4![]() t+2,
t+2,
∴t![]() .
.
∵0![]() 4,
4,
∴当四边形PQP'C为菱形时,t的值为![]() 秒.
秒.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】有一直角三角形两直角边分别为6![]() 、8
、8![]() ,在其外部拼上一个以8
,在其外部拼上一个以8![]() 为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是__________
为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
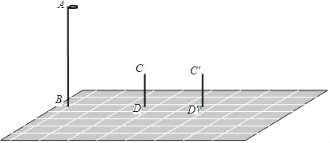
【题目】如图,AB表示路灯,CD、C′D′表示小明所在两个不同位置:
(1)分别画出这两个不同位置小明的影子;
(2)小明发现在这两个不同的位置上,他的影子长分别是自己身高的1倍和2倍,他又量得自己的身高为1.5米,DD′长为3米,你能帮他算出路灯的高度吗?(B、D、D′在一条直线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
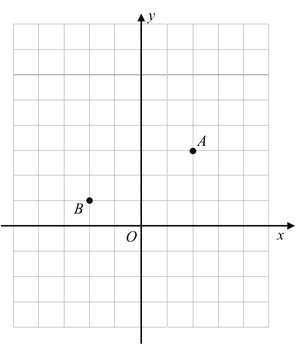
【题目】如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1).
(1)请运用所学数学知识构造图形求出AB的长;
(2)若Rt△ABC中,点C在坐标轴上,请在备用图1中画出图形,找出所有的点C后不用计算写出你能写出的点C的坐标;
(3)在x轴上是否存在点P,使PA=PB且PA+PB最小?若存在,就求出点P的坐标;若不存在,请简要说明理由(在备用图2中画出示意图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:
(1)已知,△ABC中,∠C+∠A=4∠B,∠C﹣∠A=40°,则∠A= 度;∠B= 度;∠C= 度;
(2)一个多边形的内角和与外角和之和为2160°,则这个多边形是 边形;
(3)在如图的平面直角坐标系中,点A(﹣2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小.则点P的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
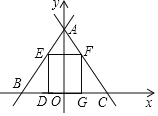
【题目】如图,直线y=kx+b与直线y=2x+6关于y轴对称且交于点A,直线y=2x+6交x轴于点B,直线y=kx+b交x轴于点C,正方形DEFG一边DG在线段BC上,点E在线段AB上,点F在线段AC上,则点G的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE。

(1)试说明△BDE≌△CDF
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com