
【题目】八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图5-1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图5-2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后1回答下列问题:
(1)方案(Ⅰ)是否可行?说明理由.
(2)方案(Ⅱ)是否可行?说明理由.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°, 方案(Ⅱ)是否成立? .
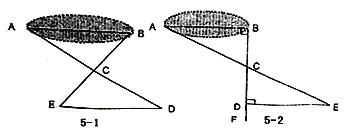
【答案】(1)见解析;(2)见解析;(3)∠ABD=∠BDE=90°,成立.
【解析】
(1)由题意可证明△ACB≌△DCE,AB=DE,故方案(Ⅰ)可行;
(2)由题意可证明△ABC≌△EDC,AB=ED,故方案(Ⅱ)可行;
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是∠ABD=∠BDE;若仅满足∠ABD=∠BDE≠90°,仍可以证明△ABC≌△EDC,则也可得到AB=ED.
(1)在△ACB和△DCE中
∵AC=DC
∠ACB=∠DCE
BC=EC
∴△ACB≌△DCE(SAS)
∴AB=DE,
故方案(Ⅰ)可行;
(2)∵CB⊥AB、CD⊥DE
∴∠ABC=∠EDC=90°
在△ABC和△EDC中
∵∠ABC=∠EDC
BC=DC
∠ACB=∠ECD
∴△ABC≌△EDC (ASA)
∴ED=AB,
故方案(Ⅱ)可行;
(3)作BF⊥AB,ED⊥BF的目的是 作∠ABC=∠EDC=90°;
如果∠ABD=∠BDE≠90°,仍可以利用ASA证明△ABC≌△EDC,则也可得到AB=ED.
故答案为:(1)见解析;(2)见解析;(3)∠ABD=∠BDE=90°,成立.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在8×8的网格中的每个小正方形边长都是1,线段交点称作格点.任意连接这些格点,可得到一些线段.按要求作图:
(1)请画出△ABC的高AD;
(2)请连接格点,用一条线段将图中△ABC分成面积相等的两部分;
(3)直接写出△ABC的面积是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
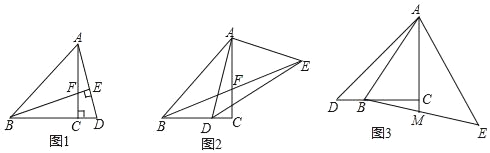
【题目】已知:△ABC中,∠ACB=90°,AC=BC.
(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;
(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;
(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
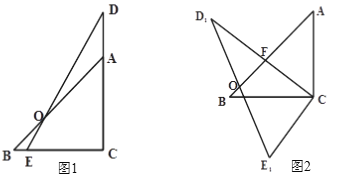
【题目】把两个直角三角形如图(1)放置,使∠ACB与∠DCE重合,AB与DE相交于点O,其中∠DCE=90°,∠BAC=45°,AB=6![]() cm,CE=5cm, CD=10cm.
cm,CE=5cm, CD=10cm.
(1)图1中线段AO的长= cm;DO=cm
(2)如图2,把△DCE绕着点C逆时针旋转α度(0°<α<90°)得△D1CE1,D1C与AB相交于点F,若△BCE1恰好是以BC为底边的等腰三角形,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一直角三角形两直角边分别为6![]() 、8
、8![]() ,在其外部拼上一个以8
,在其外部拼上一个以8![]() 为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是__________
为直角边的直角三角形,此时变成等腰三角形,则该等腰三角形的周长是__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com