
【题目】如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,AE=BD,∠B=∠CED,AE=3,DE=![]() ,则线段CE的长为_____.
,则线段CE的长为_____.

【答案】5
【解析】
过点C作CF//DE交AB的延长线于点F,设CE=x,CF=y,由DE//FC可得![]() ,可表示BF=
,可表示BF=![]() .证明△ADE∽△CFB,可得
.证明△ADE∽△CFB,可得![]() ,得出x与y的关系式①,可得
,得出x与y的关系式①,可得![]() ,则可得出x与y的关系式②,联立①②可解出x得出答案.
,则可得出x与y的关系式②,联立①②可解出x得出答案.
解:过点C作CF//DE交AB的延长线于点F,
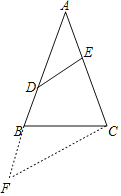
∵AB=AC,AE=BD,
∴AD=CE,
设CE=x,CF=y,
∵DE//FC,
∴![]() ,
,
∴![]() ,
,
∴BF=![]() .
.
∵∠ABC=∠CED,
∴∠AED=∠CBF,
∵DE//CF,
∴∠ADE=∠BFC,
∴△ADE∽△CFB,
∴![]() ,
,
∴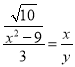 .
.
∴![]() ①
①
∵DE//CF,
∴△ADE∽△AFC,
∴![]() ,
,
∴![]() ,
,
∴![]() ②.
②.
由①②可得,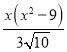 =
=![]() .
.
整理得x2﹣3x﹣10=0.
解得x=5,x=﹣2(舍去).
故答案为:5.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某销售商准备在南充采购一批丝绸,经调查,用10000元采购A型丝绸的件数与用8000元采购B型丝绸的件数相等,一件A型丝绸进价比一件B型丝绸进价多100元.
(1)求一件A型、B型丝绸的进价分别为多少元?
(2)若销售商购进A型、B型丝绸共50件,其中A型的件数不大于B型的件数,且不少于16件,设购进A型丝绸m件.
①求m的取值范围.
②已知A型的售价是800元/件,销售成本为2n元/件;B型的售价为600元/件,销售成本为n元/件.如果50≤n≤150,求销售这批丝绸的最大利润w(元)与n(元)的函数关系式(每件销售利润=售价﹣进价﹣销售成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元。
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售。设购买个x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
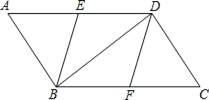
【题目】如图,在ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB运动,速度为2cm/s;动点Q从点B开始沿BC运动,速度为4cm/s.设P、Q两点同时运动,运动时间为ts(0<t<4),当△QBP与△ABC相似时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
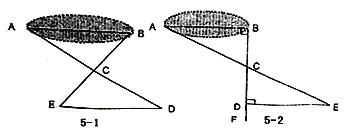
【题目】八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图5-1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图5-2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后1回答下列问题:
(1)方案(Ⅰ)是否可行?说明理由.
(2)方案(Ⅱ)是否可行?说明理由.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°, 方案(Ⅱ)是否成立? .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com