
【题目】已知:△ABC中,∠ACB=90°,AC=BC.
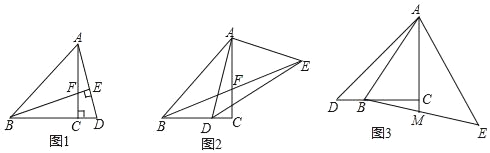
(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;
(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;
(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出![]() 的值.
的值.
【答案】(1)证明见解析;(2)结论:BD=2CF.理由见解析;(3)![]() .
.
【解析】
(1)欲证明BF=AD,只要证明△BCF≌△ACD即可;
(2)结论:BD=2CF.如图2中,作EH⊥AC于H.只要证明△ACD≌△EHA,推出CD=AH,EH=AC=BC,由△EHF≌△BCF,推出CH=CF即可解决问题;
(3)利用(2)中结论即可解决问题.
(1)证明:如图1中,
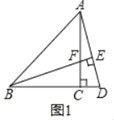
∵BE⊥AD于E,
∴∠AEF=∠BCF=90°,
∵∠AFE=∠CFB,
∴∠DAC=∠CBF,
∵BC=CA,
∴△BCF≌△ACD,
∴BF=AD.
(2)结论:BD=2CF.
理由:如图2中,作EH⊥AC于H.
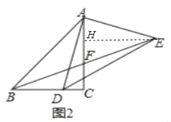
∵∠AHE=∠ACD=∠DAE=90°,
∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,
∴∠DAC=∠AEH,
∵AD=AE,
∴△ACD≌△EHA,
∴CD=AH,EH=AC=BC,
∵CB=CA,
∴BD=CH,
∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,
∴△EHF≌△BCF,
∴FH=CF,
∴BC=CH=2CF.
(3)如图3中,同法可证BD=2CM.
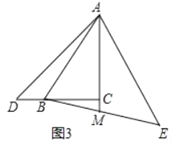
∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,
∴![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
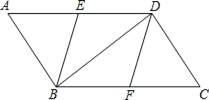
【题目】如图,在ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
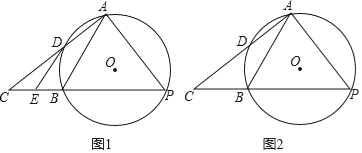
【题目】已知AB是⊙O的弦,点P是优弧AB上的一个动点,连接AP,过点A作AP的垂线,交PB的延长线于点C.
(1)如图1,AC与⊙O相交于点D,过点D作⊙O的切线,交PC于点E,若DE∥AB,求证:PA=PB;
(2)如图2,已知⊙O的半径为2,AB=2![]() .
.
①当点P在优弧AB上运动时,∠C的度数为 °;
②当点P在优弧AB上运动时,△ABP的面积随之变化,求△ABP面积的最大值;
③当点P在优弧AB上运动时,△ABC的面积随之变化,△ABC的面积的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )

A.①②③④B.②③④⑤C.①③④⑤D.①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
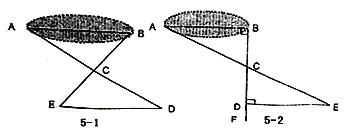
【题目】八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图5-1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图5-2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后1回答下列问题:
(1)方案(Ⅰ)是否可行?说明理由.
(2)方案(Ⅱ)是否可行?说明理由.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°, 方案(Ⅱ)是否成立? .
查看答案和解析>>
科目:初中数学 来源: 题型:
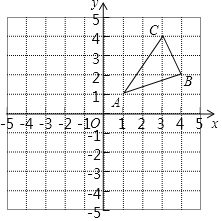
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)P为x轴上一动点,当AP+CP有最小值时,求这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
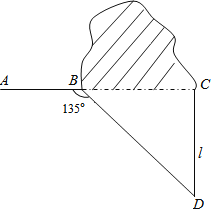
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com