
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )

A.①②③④B.②③④⑤C.①③④⑤D.①②③⑤
【答案】D
【解析】
①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE;
②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;
③根据②△CQB≌△CPA(ASA),可知③正确;
④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;
⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.
解:∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴①正确,
∵△ACD≌△BCE,
∴∠CBE=∠DAC,
又∵∠ACB=∠DCE=60°,
∴∠BCD=60°,即∠ACP=∠BCQ,
又∵AC=BC,
∴△CQB≌△CPA(ASA),
∴CP=CQ,
又∵∠PCQ=60°可知△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE②正确,
∵△CQB≌△CPA,
∴AP=BQ③正确,
∵AD=BE,AP=BQ,
∴AD-AP=BE-BQ,
即DP=QE,
∵∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,故④错误;
∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵等边△DCE,
∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,
∴⑤正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是x和y,由题意得方程组: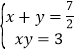 ,消去y化简得:2x2﹣7x+6=0,
,消去y化简得:2x2﹣7x+6=0,
∵△=49﹣48>0,
∴x1=_____,x2=_______,
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
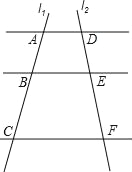
【题目】如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,![]() ,AC=14;
,AC=14;
(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
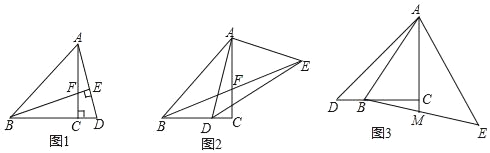
【题目】已知:△ABC中,∠ACB=90°,AC=BC.
(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;
(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;
(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC=3MC,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
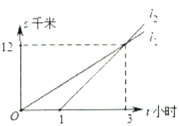
【题目】如图,![]() 两地相距
两地相距![]() 千米,甲、乙两人都从
千米,甲、乙两人都从![]() 地去
地去![]() 地,图中
地,图中![]() 和
和![]() 分别表示甲、乙两人所走路程
分别表示甲、乙两人所走路程![]() (千米)与时间
(千米)与时间![]() (小时)之间的关系,下列说法: ①乙晚出发
(小时)之间的关系,下列说法: ①乙晚出发![]() 小时;②乙出发
小时;②乙出发![]() 小时后追上甲;③甲的速度是
小时后追上甲;③甲的速度是![]() 千米/小时; ④乙先到达
千米/小时; ④乙先到达![]() 地.其中正确的是__________.(填序号)
地.其中正确的是__________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com