
【题目】为迎接北京2022年冬奥会,某工艺厂准备生产奥运会标志与奥运会吉祥物,该厂主要用甲、乙两种原料.已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完.
(1)求该厂能生产奥运会标志和奥运会吉祥物各多少套?
(2)如果奥运会标志的成本为16元,奥运会吉祥物的成本为15元,若东营客商购进奥运会标志和奥运会吉祥物共250件进行试销,其中奥运会标志的件数不大于奥运会吉祥物的件数,且不小于80件,已知奥运会标志的售价为24元/件,奥运会吉祥物的售价为22元/件,且全部售出,设购进奥运会标志m件,求该客商销售这批商品的利润y与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,东营客商决定在试销活动中毎售出一件奥运会标志,就从一件奥运会标志的利润中捐献慈善资金a元,求该客商售完所有商品并捐献资金后获得的最大收益.
【答案】(1)该厂能生产奥运会标志2000套,能生产奥运会吉祥物2400套;(2)80≤m≤125;(3)当m=80时,w取最大值,最大收益为[80(1﹣a)+1750]元.
【解析】
(1)设该厂能生产奥运会标志x套,能生产奥运会吉祥物z套,根据该厂购进甲、乙原料的数量,即可得出关于x、z的二元一次方程,解之即可得出结论;
(2)设购进奥运会标志m件,则购进奥运会吉祥物(250﹣m)件,根据总利润=单价利润×购进数量,即可得出y关于m的函数关系式,再由奥运会标志的件数不大于奥运会吉祥物的件数且不小于80件,即可得出m的取值范围;
(3)设该客商售完所有商品并捐献资金后获得的收益为w元,根据收益=利润﹣捐献总资金,即可得出w关于m的函数关系式,再利用一次函数的性质即可解决最值问题.
(1)设该厂能生产奥运会标志x套,能生产奥运会吉祥物z套,
根据题意得:![]() ,
,
解得:![]() .
.
答:该厂能生产奥运会标志2000套,能生产奥运会吉祥物2400套.
(2)设购进奥运会标志m件,则购进奥运会吉祥物(250﹣m)件,
根据题意得:y=(24﹣16)m+(22﹣15)(250﹣m)=m+1750.
∵奥运会标志的件数不大于奥运会吉祥物的件数,且不小于80件,
∴![]() ,
,
∴80≤m≤125.
(3)设该客商售完所有商品并捐献资金后获得的收益为w元,
根据题意得:w=y﹣am=(1﹣a)m+1750(80≤m≤125),
∴①当a<1时,1﹣a>0,
∴w随m值的增大而增大,
∴当m=125时,w取最大值,最大收益为[125(1﹣a)+1750]元;
②当a=1时,1﹣a=0,
∴w=1750,即在80≤m≤125中,该客商均为1750元;
③当a>1时,1﹣a<0,
∴w随x值的增大而减小,
∴当m=80时,w取最大值,最大收益为[80(1﹣a)+1750]元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点B(-![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点(不与
边上一点(不与![]() 重合),以
重合),以![]() 为直径作
为直径作![]() ,过
,过![]() 作
作![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
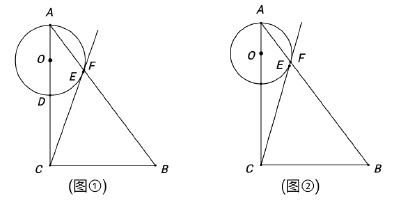
(1)若![]() 的半径为2,求线段
的半径为2,求线段![]() 的长;
的长;
(2)若![]() ,求
,求![]() 的半径;
的半径;
(3)如图②,若![]() ,点
,点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,试求
,试求![]() 、
、![]() 两点之间的距离.
两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】历下区历史文化悠久,历下一名,取意于大舜帝耕作于历山之下。这位远古圣人为济南留下了影响深远的大舜文化,至今已绵延两千年.某校就同学们对“舜文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图:
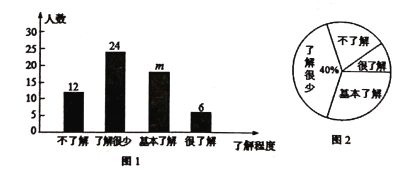
根据统计图的信息,解答下列问题:
(1)本次共调查 名学生,条形统计图中![]() ;
;
(2)若该校共有学生1200名,请估算该校约有多少名学生不了解“舜文化”;
(3)谓查结果中,该校九年级(2)班有四名同学相当优秀,了解程度为“很了解”,他们是三名男生、—名女生,现准备从这四名同学中随机抽取两人去市里参加“舜文化”知识竞赛,用树状或列表法,求恰好抽中一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:在一次数学社团活动课上,同学们测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进100米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD的高度.(保留根号)
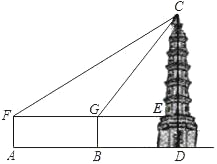
查看答案和解析>>
科目:初中数学 来源: 题型:
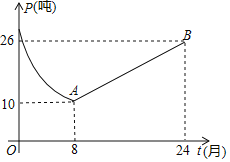
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com